Тест ЕГЭ по профильной математике решать онлайн

1. В треугольнике со сторонами 15 и 5 проведены высоты к этим сторонам. Высота, проведённая к первой из этих сторон, равна 1. Чему равна высота, проведённая ко второй стороне?

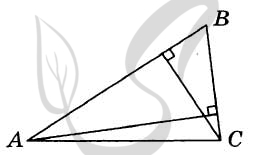
Верный ответ: 3

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10178.

2. На координатной плоскости изображены векторы $ \vec a $ и $ \vec b $. Найдите косинус угла между векторами $ \vec a $ и $ \vec b $.

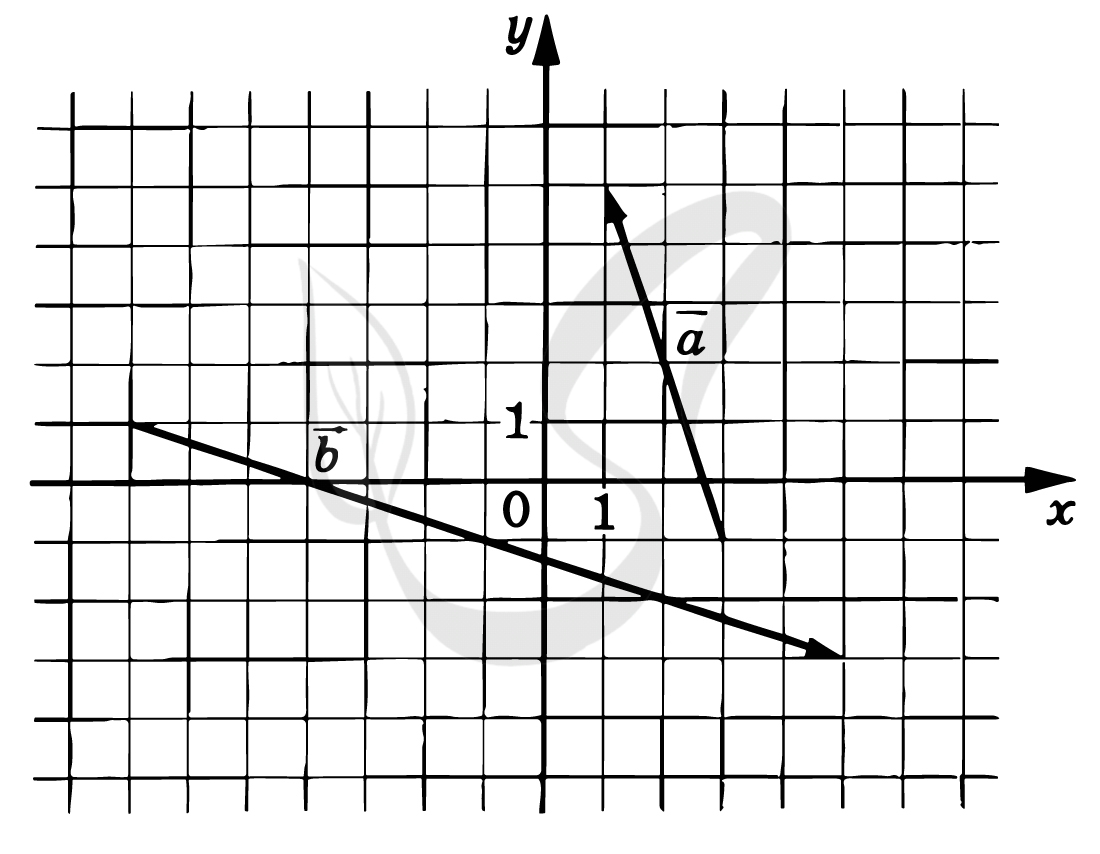
Верный ответ: -0,6

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21348.

3. В сосуде, имеющем форму конуса, уровень жидкости достигает $ \frac{1}{3} $ высоты. Объём жидкости равен 4 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

Верный ответ: 104

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10427.

4. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что произведение выпавших очков делится на 5, но не делится на 30.

Верный ответ: 0,25

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10442.

5. Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 8. Какова вероятность того, что для этого потребовалось два броска? Округлите ответ до сотых.

Верный ответ: 0,28

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 15354.

6. Найдите корень уравнения $ \sqrt {\frac{{2x + 5}}{3}} = 5 $.

Верный ответ: 35

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10158.

7. Найдите значение выражения $ \sqrt {200} \cdot {\cos ^2}\frac{{5\pi }}{8} - \sqrt {50} $.

Верный ответ: -5

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10295.

8. На рисунке изображён график $ y = f'(x) $ - производной функции $ f(x) $, определённой на интервале $ (-5; 5) $. Найдите количество точек максимума функции $ f(x) $, принадлежащую отрезку $ [-3; 4] $.

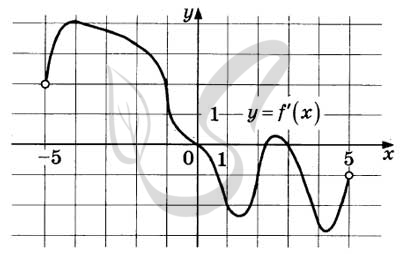
Верный ответ: 2

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10160.

9. Скорость движения автомобиля $ \upsilon $ (км/ч) и угловая скорость вращения вала двигателя $ {\omega _{двиг.}} $ (об/мин) связаны соотношением $$ \upsilon = \frac{{0,0006 \cdot \pi d{\omega _{двиг.}}}}{{kb}} $$ где $d $ - диаметр колеса (см), $k $ - передаточное число дифференциала автомобиля, $b $ - передаточное число коробки передач при выбранной передаче. В таблице указаны передаточные числа для автомобиля «Лада-Калина».

У автомобиля «Лада-Калина» диаметр колеса равен 56 см. Водитель двигается на 1-й передаче с постоянной скоростью. Прибор (тахометр) показывает, что число оборотов двигателя равно 4000 об/мин. Считайте, что $ \pi $ = 3,14. Найдите скорость автомобиля в км/ч. Результат округлите до целого значения.

Верный ответ: 31

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10144.

10. Семь одинаковых рубашек дешевле куртки на 2%. На сколько процентов десять таких же рубашек дороже куртки?

Верный ответ: 40

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10487.

11. На рисунке изображён график функции $ f(x) = a{x^2} - 8x + c $. Найдите $ f( - 2) $.

Верный ответ: 27

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 15353.

12. Найдите наименьшее значение функции $ y = 4x - \ln (4x) + 16 $ на отрезке $ \left[ {\frac{1}{8};\frac{5}{8}} \right] $.

Верный ответ: 17

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10279.

Часть 2

13. Выполните следующие пункты:

а) Решите уравнение $ 2 - 5\cos x - \cos 2x = 0 $.
б) Найдите его корни, принадлежащие отрезку $ \left[ { - \frac{{5\pi }}{2}; - \pi } \right] $.

а) $ \pm \frac{\pi }{3} + 2\pi k,k \in Z $

б) $ - \frac{{7\pi }}{3}; - \frac{{5\pi }}{3} $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10185.

14. В правильной треугольной призме ABCA₁B₁C₁ все рёбра равны 1.
а) Докажите, что прямая AB₁, параллельна прямой, проходящей через середины отрезков AC и BC₁.
б) Найдите косинус угла между прямыми AB₁ и BC₁.

б) $ \frac{1}{4} $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10300.

15. Решите неравенство $ \frac{{{x^2} - 2x - 1}}{{x - 2}} + \frac{2}{{x - 3}} \le x $.

$ \left( { - \infty ;1} \right];\left( {2;3} \right) $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10206.

16. 31 декабря 2014 года Василий взял в банке некоторую сумму в кредит под 11% годовых. Схема выплаты кредита следующая - 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 11%), затем Василий переводит в банк 3 696 300 рублей. Какую сумму взял Василий в банке, если он выплатил долг двумя равными платежами (то есть за два года)?

6 330 000 рублей

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10246.

17. Дан остроугольный треугольник ABC. Биссектриса внутреннего угла при вершине B пересекает биссектрису внешнего угла при вершине C в точке M, а биссектриса внутреннего угла при вершине C пересекает биссектрису внешнего угла при вершине B в точке N.
а) Докажите, что 2$ \angle $CNM = $ \angle $ABC.
6) Найдите CN, если AB = AC = 13, BC = 10.

б) $ 6\sqrt {13} $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10131.

18. Найдите все значения $ a $, при каждом из которых уравнение $$ {\left( {3{x^2} - 3x + {a^2} + 9} \right)^2} = 12{a^2}\left( {{x^2} - x + 3} \right) $$ имеет ровно один корень.

$ a = \pm \frac{{\sqrt {33} }}{2} $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10456.

19. Имеется 8 карточек. На них записывают по одному каждое из чисел -1, 2, 4, -6, 7, -8, -10, 12. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел -1, 2, 4, -6, 7, -8, -10, 12. После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают.
а) Может ли в результате получиться 0?
б) Может ли в результате получиться 1?
в) Какое наименьшее целое неотрицательное число может в результате получиться?

а) нет
б) нет
в) 16

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10343.

Интеллектуальный и эстетичный кабинет для подготовки к ЕГЭ

Часть 2