Тест ЕГЭ по профильной математике решать онлайн

1. В треугольнике ABC угол C равен 90°, AB = 14, $ tgA = \frac{20}{ 3\sqrt {10}} $. Найдите AC.

Верный ответ: 6

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10463.

2. Даны векторы $ \vec a $(6;-1), $ \vec b $(-5;-2) и $ \vec c $(-3;5). Найдите длину вектора $ \vec a - \vec b + \vec c $.

Верный ответ: 10

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21349.

3. Диагональ правильной четырёхугольной призмы наклонена к плоскости основания под углом 30°. Боковое ребро равно 6. Найдите диагональ призмы.

Верный ответ: 12

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10332.

4. Клиент получает в банке кредитную карту. Четыре последние цифры номера карты случайные. Какова вероятность того, что эти последние четыре цифры состоят из двух повторяющихся групп по 2 различные цифры, например 0404 или 5252?

Верный ответ: 0,009

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10119.

5. Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 4. Какова вероятность того, что для этого потребовалось два броска?

Верный ответ: 0,5

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 15356.

6. Найдите корень уравнения $ {\log _2}( - 2 - x) = 1 $.

Верный ответ: -4

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10310.

7. Найдите значение выражения $ ({246^2} - {17^2}):263 $.

Верный ответ: 229

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10428.

8. На рисунке изображён график функции $ y = f(x) $, определённой на интервале (-6; 6). Найдите количество решений уравнения $ f'(x) = 0 $ на отрезке [-5,5; 4].

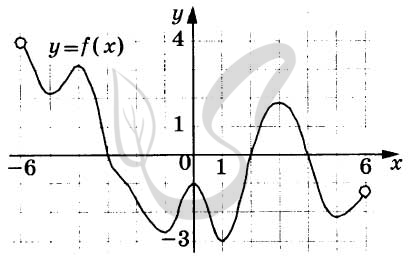
Верный ответ: 6

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10293.

9. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием $ f $ = 28 см. Расстояние ${d_1}$, от линзы до лампочки может изменяться в пределах от 40 до 60 см, а расстояние ${d_2}$, от линзы до экрана - в пределах от 53 до 77 см. Изображение на экране будет чётким, если выполнено соотношение $ \frac{1}{{{d_1}}} + \frac{1}{{{d_2}}} = \frac{1}{f} $. Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы её изображение на экране было чётким. Ответ дайте в сантиметрах.

Верный ответ: 44

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10315.

10. Девять одинаковых рубашек дешевле куртки на 7%. На сколько процентов двенадцать таких же рубашек дороже куртки?

Верный ответ: 24

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10506.

11. На рисунке изображён график функции $ f(x) = a{x^2} - 3x + c $. Найдите $ f(5) $.

Верный ответ: -61

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 15355.

12. Найдите наибольшее значение функции $ y = {x^5} + 20{x^3} - 65x $ на отрезке $ \left[ { - 4;0} \right] $.

Верный ответ: 44

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10241.

Часть 2

13. Выполните следующие пункты:

а) Решите уравнение $ \frac{{2{{\sin }^2}x - \sin x}}{{2\cos x - \sqrt 3 }} = 0 $.
б) Найдите все корни этого уравнения, принадлежащие отрезку $ \left[ {\frac{{3\pi }}{2};3\pi } \right] $.

а) $ \pi n;\frac{{5\pi }}{6} + 2\pi n,n \in Z $

б) $ 2\pi ;\frac{{17\pi }}{6};3\pi $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10318.

14. В основании прямой призмы ABCA₁B₁C₁ лежит прямоугольный треугольник ABC с прямым углом C. Точка M - середина ребра B₁C₁, точка N лежит на ребре AC, причём AN : NC = 15 : 1. Катет AC в четыре раза больше бокового ребра AA₁ призмы.
а) Докажите, что прямая MN перпендикулярна прямой CA₁.
б) Найдите угол между прямой MN и плоскостью основания A₁B₁C₁, если $ \cos \angle CBA = \frac{1}{{\sqrt 5 }} $.

б) $ arctg\frac{{4\sqrt {17} }}{{17}} $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10110.

15. Решите неравенство $ 2x \ge {\log _3}\left( {\frac{{35}}{2} \cdot {6^{x - 1}} - 3 \cdot {4^{x - \frac{1}{2}}}} \right) $.

$ \left( {{{\log }_{\frac{3}{2}}}\frac{{18}}{{35}}; - 1} \right];\left[ {2; + \infty } \right) $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10130.

16. Планируется выдать льготный кредит на целое число миллионов рублей на пять лет. В середине каждого года действия кредита долг заёмщика возрастает на 20% по сравнению с началом года. В конце 1-го, 2-го и 3-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наибольший размер кредита, при котором общая сумма выплат заёмщика будет меньше 9 млн руб.

4 млн рублей

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10151.

17. На катетах AC и BC прямоугольного треугольника ABC вне треугольника построены квадраты ACDE и BFKC. Точка M - середина гипотенузы AB, H - точка пересечения прямых CM и DK.
а) Докажите, что прямые CM и DK перпендикулярны.
б) Найдите MH, если известно, что катеты треугольника ABC равны 30 и 40.

б) 49

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10340.

18. Найдите все значения $ a $, при каждом из которых уравнение $$ {\left( {2{x^2} + x + 3{a^2} + 5} \right)^2} = 12{a^2}\left( {2{x^2} + x + 5} \right) $$ имеет ровно один корень.

$ a = \pm \frac{{\sqrt {26} }}{4} $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10418.

19. а) Приведите пример такого натурального числа $ n $, что числа $ {n^2} $ и $ {(n + 16)^2} $ дают одинаковый остаток при делении на 200.
б) Сколько существует трёхзначных чисел $ n $ с указанным в пункте $ a $ свойством?
в) Сколько существует двузначных чисел $ m $, для каждого из которых существует ровно 36 трёхзначных чисел $ n $, таких, что $ {n^2} $ и $ {(n + m)^2} $ дают одинаковый остаток при делении на 200?

а) 17
б) 36
в) 18

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10305.

Интеллектуальный и эстетичный кабинет для подготовки к ЕГЭ

Часть 2