Тест ЕГЭ по профильной математике решать онлайн

1. В треугольнике ABC угол C равен 66°, стороны AC и BC равны. Найдите угол A. Ответ дайте в градусах.

Верный ответ: 57

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10501.

2. Даны векторы $ \vec a $(-1;3), $ \vec b $(4;1) и $ \vec c $(2; $ {c_0} $). Найдите $ {c_0} $, если $ \left( {\vec a + \vec b} \right) \cdot \vec c = 0 $.

Верный ответ: -1,5

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21353.

3. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известны длины рёбер: AB = 3, AD = 4, AA₁ = 32. Найдите площадь сечения, проходящего через вершины C, C₁ и A.

Верный ответ: 160

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10256.

4. Девять детей встают в хоровод в случайном порядке. Среди них Серёжа и его сестра Маша. Какова вероятность того, что Серёжа и Маша окажутся рядом?

Верный ответ: 0,25

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10480.

5. Маша коллекционирует принцесс из Киндер-сюрпризов. Всего в коллекции 10 разных принцесс, и они равномерно распределены, то есть в каждом очередном Киндер-сюрпризе может с равными вероятностями оказаться любая из 10 принцесс. У Маши уже есть четыре разные принцессы из коллекции. Какова вероятность того, что для получения следующей принцессы Маше придётся купить ещё 1 или 2 шоколадных яйца?

Верный ответ: 0,84

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 15364.

6. Найдите корень уравнения $ {\left( {\frac{1}{4}} \right)^{13 - 5x}} = {16^{3x}} $.

Верный ответ: -13

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10443.

7. Найдите значение выражения $ 2 (p(6x) - 6p(x+5)) $, если $ p(x) = x + 2 $.

Верный ответ: -80

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10124.

8. На рисунке изображён график $ y = f'(x) $ - производной функции $ f(x) $, определённой на интервале $ (-1; 11) $. Найдите точку экстремума функции $ f(x) $, принадлежащую отрезку $ [2; 8] $.

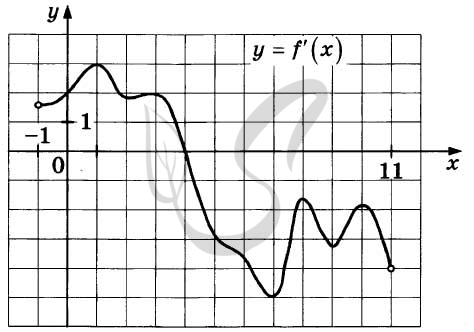
Верный ответ: 4

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10122.

9. На рисунке изображена схема вантового моста. Вертикальные пилоны связаны провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами. Введём систему координат: ось $ Oy $ направим вертикально вдоль одного из пилонов, а ось $ Ox $ направим вдоль полотна моста, как показано на рисунке. В этой системе координат линия, по которой провисает цепь моста, имеет уравнение $ y = 0,0013{x^2} - 0,35x + 27 $, где $ x $ и $ y $ измеряются в метрах. Найдите длину ванты, расположенной в 30 метрах от пилона. Ответ дайте в метрах.

Верный ответ: 17,67

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10220.

10. Расстояние между городами A и B равно 440 км. Из города A в город B выехал первый автомобиль, а через два часа после этого навстречу ему из города В выехал со скоростью 90 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 260 км от города A. Ответ дайте в км/ч.

Верный ответ: 65

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10297.

11. На рисунке изображён график функции $ f(x) = \frac{k}{x} + a $. Найдите $ f(-12) $.

Верный ответ: 0,75

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 15363.

12. Найдите наибольшее значение функции $ f(x) = - {x^3} + 3{x^2} + 9x - 29 $ на отрезке $ [ - 1;4] $.

Верный ответ: -2

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10222.

Часть 2

13. Выполните следующие пункты:

а) Решите уравнение $ \cos x = \sqrt {\frac{{1 + \sin x}}{2}} $.
б) Найдите его корни, принадлежащие отрезку $ \left[ {3\pi ;\frac{{9\pi }}{2}} \right] $.

а) $ - \frac{\pi }{2} + 2\pi k,k \in Z; - \frac{\pi }{6} + 2\pi k,k \in Z $

б) $ \frac{{7\pi }}{2};\frac{{25\pi }}{6} $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10413.

14. В основании пирамиды SABCD лежит прямоугольник ABCD со стороной AB = 3 и диагональю BD = 5. Все боковые рёбра пирамиды равны 3. На отрезке BD отмечена точка E, а на ребре AS - точка F так, что SF = BE = 2.
а) Докажите, что плоскость CEF параллельна ребру SB.
а) Плоскость CEF пересекает ребро SD в точке Q. Найдите расстояние от точки Q до плоскости ABC.

б) $ \frac{{3\sqrt {11} }}{{20}} $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10167.

15. Решите неравенство $ {4^{x + 1}} - 17 \cdot {2^x} + 4 \le 0 $.

[-2;2]

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10263.

16. 31 декабря 2016 года Виктор взял в банке 3 972 000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая - 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Виктор переводит в банк $ x $ рублей. Каким должно быть число $ x $, чтобы Виктор выплатил долг тремя равными платежами (то есть за три года)?

1 597 200 рублей

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10512.

17. Прямая, проходящая через середину M гипотенузы AB прямоугольного треугольника ABC, перпендикулярна CM и пересекает катет AC в точке K. При этом AK : KC = 1 : 2.
а) Докажите, что $ \angle $ВАС = 30°.
б) Пусть прямые MK и BC пересекаются в точке P, а прямые AP и BK - в точке Q. Найдите KQ, если BC = $ 3\sqrt 14 $.

б) $ 14\sqrt 6 $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10473.

18. Найдите все значения а, при каждом из которых система $$ \left\{ \begin{array}{l} \left| {{x^2} - x - 6} \right| = {(y - 1)^2} + x - 7\\ 3y = 2x + a \end{array} \right. $$ имеет ровно один или два корня.

$ \left( { - 9; - 2} \right];\left[ {3; + \infty } \right) $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10247.

19. На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 363. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71).
а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 4 раза больше, чем сумма исходных чисел.
б) Могла ли сумма получившихся чисел быть ровно в 2 раза больше, чем сумма исходных чисел?
в) Найдите наибольшее возможное значение суммы получившихся чисел.

а) например, 15 раз число 19 и число 78
б) нет
в) 1650

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10248.

Интеллектуальный и эстетичный кабинет для подготовки к ЕГЭ

Часть 2