Тест ЕГЭ по профильной математике решать онлайн

1. В прямоугольном треугольнике угол между высотой и медианой, проведёнными из вершины прямого угла, равен 32°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.

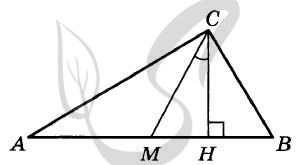
Верный ответ: 61

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10311.

2. На координатной плоскости изображены векторы $ \vec a $, $ \vec b $ и $ \vec c $. Найдите длину вектора $ \vec a + \vec b - \vec c $.

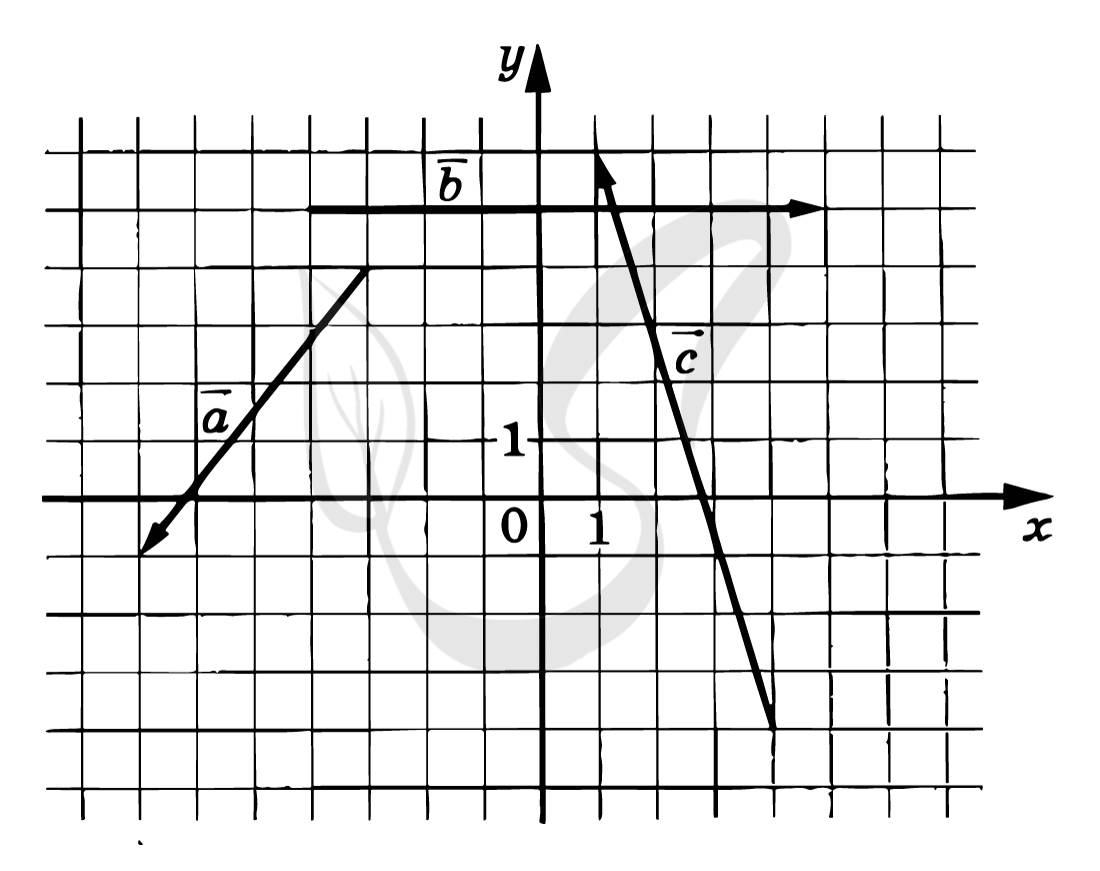
Верный ответ: 17

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21355.

3. Шар вписан в цилиндр. Площадь поверхности шара равна 10. Найдите площадь полной поверхности цилиндра.

Верный ответ: 15

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10180.

4. Клиент получает в банке кредитную карту. Четыре последние цифры номера карты случайные. Какова вероятность того, что эти последние четыре цифры идут подряд в порядке возрастания, например 0123 или 4567?

Верный ответ: 0,0007

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10100.

5. Первый член последовательности целых чисел равен 0. Каждый следующий член последовательности с вероятностью $ p = \frac{{10}}{{19}} $ на единицу больше предыдущего и с вероятностью $ 1 - p $ на единицу меньше предыдущего. Какова вероятность того, что какой-то член этой последовательности окажется равен -1?

Верный ответ: 0,9

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 15368.

6. Найдите корень уравнения $ {\log _3}(2 - x) = 2 $.

Верный ответ: -7

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10367.

7. Найдите значение выражения $ - 32\sqrt 3 tg( - 600^\circ ) $.

Верный ответ: 96

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10504.

8. На рисунке изображён график функции y = f(x) и отмечены точки -7, -3, 1, 7. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

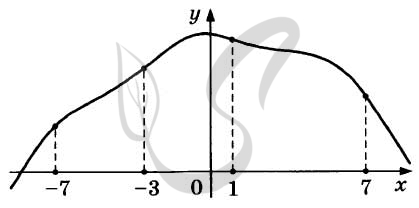
Верный ответ: 7

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10236.

9. Наблюдатель, находящийся на высоте $ h $ м над поверхностью земли, видит линию горизонта на расстоянии $ l $ км, которое можно найти по формуле $ l = \sqrt {\frac{{Rh}}{{500}}} $‚ где $ R $ = 6400 км - радиус Земли.
Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 километра. К пляжу ведет лестница, каждая ступенька которой имеет высоту 20 см. На сколько ступенек ему нужно подняться, чтобы он увидел горизонт на расстоянии 6,4 километра?

Верный ответ: 7

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10429.

10. Первый и второй насосы наполняют бассейн за 9 минут, второй и третий - за 12 минут, а первый и третий - за 18 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?

Верный ответ: 8

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10164.

11. На рисунке изображён график функции $ f(x) = \frac{k}{x} + a $. Найдите $ f\left( {\frac{1}{3}} \right) $.

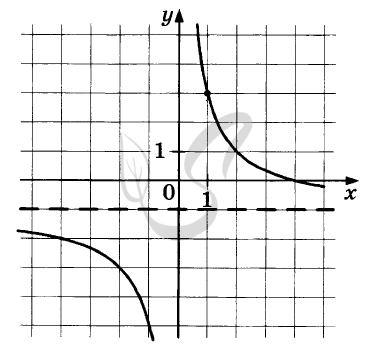
Верный ответ: 11

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 15367.

12. Найдите точку максимума функции $ y = - \frac{x}{{{x^2} + 625}} $.

Верный ответ: -25

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10450.

Часть 2

13. Выполните следующие пункты:

а) Решите уравнение $ 2{\sin ^4}x + 3\cos 2x + 1 = 0 $.
б) Найдите все корни этого уравнения, принадлежащие отрезку $ \left[ {\pi ;3\pi } \right] $.

а) $ \frac{\pi }{2} + \pi n,n \in Z $

б) $ \frac{{3\pi }}{2};\frac{{5\pi }}{2} $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10375.

14. На ребре AA₁ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁, взята точка E так, что A₁E : EA = 3 : 1, на ребре BB₁ - точка F так, что B₁F : FB = 1 : 3, а на ребре B₁C₁, точка T так, что B₁T : TC₁ = 1 : 2. Известно, что AB = 4, AD = 3, AA₁ = 4.
а) Докажите, что плоскость EFT проходит через вершину D₁.
б) Найдите угол между плоскостью EFT и плоскостью BB₁C₁.

б) $ \arccos \frac{1}{3} $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10395.

15. Решите неравенство $ {\log _3}\frac{1}{x} + {\log _3}({x^2} + 3x - 9) $ $ \le {\log _3}\left( {{x^2} + 3x + \frac{1}{x} - 10} \right) $.

$ \left[ {2; + \infty } \right) $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10320.

16. 15 января планируется взять кредит в банке на 5 месяцев. Условия его возврата таковы:
- 1-го числа каждого месяца долг возрастает на 5% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования?

115

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10398.

17. Прямая, проходящая через середину M гипотенузы AB прямоугольного треугольника ABC, перпендикулярна CM и пересекает катет AC в точке K. При этом AK : KC = 1 : 2.
а) Докажите, что $ \angle $ВАС = 30°.
б) Пусть прямые MK и BC пересекаются в точке P, а прямые AP и BK - в точке Q. Найдите KQ, если BC = $ 4\sqrt 6 $.

б) $ 8\sqrt {14} $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10416.

18. Найдите все значения $a $, при каждом из которых уравнение $$ {x^4} - 4{x^3} - 6{x^2} + 4ax + 6a - {a^2} = 0 $$ имеет не менее трёх корней.

$ 0 \le a \le 10 $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10133.

19. Конечная возрастающая последовательность ${a_1}$, ${a_2}$, ... , ${a_n}$, состоит из n $ \ge $ 3 различных натуральных чисел, причём при всех натуральных $ k \le n - 2 $ выполнено равенство $ 6{a_{k + 2}} = 7{a_{k + 1}} - {a_k} $.
а) Приведите пример такой последовательности при $ n $ = 5.
б) Может ли в такой последовательности при некотором $n$ $ \ge $ 3 выполняться равенство $ 5{a_n} = 6{a_2} - {a_1} $ ?
в) Какое наименьшее значение может принимать ${a_1}$, если ${a_n}$ = 404?

а) например последовательность 1, 433, 505, 517, 519
б) нет
в) 5

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10457.

Интеллектуальный и эстетичный кабинет для подготовки к ЕГЭ

Часть 2