Тест ЕГЭ по профильной математике решать онлайн

1. В треугольнике ABC AC = BC, угол C равен 120°, AB = $ \sqrt 3 $. Найдите AC.

Верный ответ: 1

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10216.

2. Даны векторы $ \vec a $(-2; 4) и $ \vec b $(2; -1). Известно, что векторы $ \vec c({x_c};{y_c}) $ и $ {\vec b} $ сонаправленные, а $ \left| {\vec c} \right| = \left| {\vec a} \right| $. Найдите $ {x_c} + {y_c} $ .

Верный ответ: 2

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21357.

3. Шар вписан в цилиндр. Площадь поверхности шара равна 30. Найдите площадь полной поверхности цилиндра.

Верный ответ: 45

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10161.

4. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что разница выпавших очков равна 1 или 2.

Верный ответ: 0,5

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10385.

5. Первый игральный кубик обычный, а на гранях второго кубика нет чётных чисел, а нечётные числа 1, 3 и 5 встречаются по два раза. В остальном кубики одинаковые. Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 3 и 5 очков. Какова вероятность того, что бросали первый кубик?

Верный ответ: 0,2

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 15372.

6. Найдите корень уравнения $ \sqrt[3]{{x - 3}} = 2 $.

Верный ответ: 11

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10234.

7. Найдите значение выражения $ \frac{{2\cos 28^\circ }}{{\cos 152^\circ }} $.

Верный ответ: -2

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10314.

8. На рисунке изображены график функции $ y = f(x) $ и касательная к нему в точке с абсциссой ${x_0}$. Найдите значение производной функции $ f(x) $ в точке ${x_0}$.

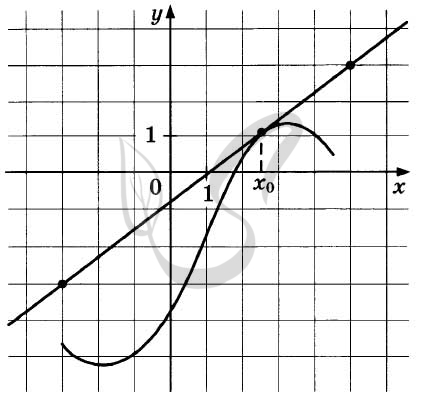
Верный ответ: 0,75

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10274.

9. Ёмкость высоковольтного конденсатора в телевизоре C = 3 ⋅ 10^-6 Ф. Параллельно с конденсатором подключён резистор с сопротивлением $ R $ = 5 ⋅ 10⁶ Ом. Во время работы телевизора напряжение на конденсаторе ${U_0}$ = 9 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения $U $ (кВ) за время, определяемое выражением $ t = \alpha RC{\log _2}\frac{{{U_0}}}{U} $ (с), где $ \alpha = 1,1\frac{с}{{Ом \cdot Ф}} $ - постоянная. Определите напряжение на конденсаторе, если после выключения телевизора прошло 33 секунды. Ответ дайте в кВ (киловольтах).

Верный ответ: 2,25

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10334.

10. Первая труба пропускает на 2 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объёмом 588 литров она заполняет на 7 минут быстрее, чем первая труба заполняет резервуар объёмом 728 литров?

Верный ответ: 28

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10145.

11. На рисунке изображён график функции $ f(x) = \frac{k}{x} + a $. Найдите $ f\left( {25} \right) $.

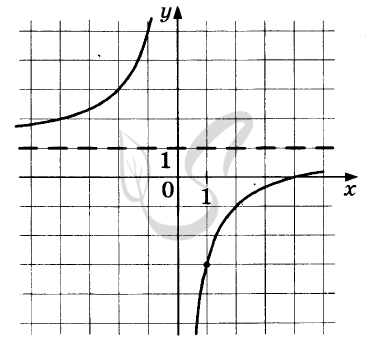
Верный ответ: 0,84

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 15371.

12. Найдите наименьшее значение $ y = 7x - 6\sin x + 12 $ на отрезке $ \left[ {0;\frac{\pi }{2}} \right] $.

Верный ответ: 12

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10127.

Часть 2

13. Выполните следующие пункты:

а) Решите уравнение $ \frac{{{{\left( {x + 3} \right)}^2}}}{5} + \frac{{20}}{{{{\left( {x + 3} \right)}^2}}} = $ $ 8\left( {\frac{{x + 3}}{5} - \frac{2}{{x + 3}}} \right) + 1 $.
б) Найдите его корни, принадлежащие отрезку $ \left[ { - 6; - 4} \right] $.

а) $ - 5;~2;~\frac{{ - 1 \pm \sqrt {65} }}{2} $

б) $ - 5;~ - \frac{{1 + \sqrt {65} }}{2} $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10508.

14. На ребре AA₁ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ взята точка E так, что A₁E : EA = 4 : 3, на ребре BB₁ - точка F так, что B₁F : FB = 2 : 5, а на ребре B₁C₁ - точка T - средина ребра B₁C₁. Известно, что AB = 3, AD = 4, AA₁ = 7.
а) Докажите, что плоскость EFT проходит через вершину D₁.
б) Найдите угол между плоскостью EFT и плоскостью BB₁C₁.

б) $ \arccos \sqrt {\frac{2}{{11}}} $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10452.

15. Решите неравенство $ {7^{\ln ({x^2} - 2x)}} \le {(2 - x)^{\ln 7}} $.

[-1; 0)

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10377.

16. У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 300 ц/га, а на втором - 200 ц/га. Урожайность свёклы на первом поле составляет 200 ц/га, а на втором - 300 ц/га. Фермер может продавать картофель по цене 10 000 руб. за центнер, а свёклу - по цене 13 000 руб. за центнер. Какой наибольший доход может получить фермер?

69 000 000 рублей

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10303.

17. В трапеции ABCD основания AD и BC. Диагональ AC разбивает её на два равнобедренных треугольника с основаниями AD и AB.
а) Докажите, что луч DB - биссектриса угла ADC.
б) Найдите AB, если известны длины диагоналей трапеции: BD = 12 и AC = 7,5.

б) 9

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10511.

18. Найдите все значения $a $, при каждом из которых уравнение $$ {x^4} + 4{x^3} + 4ax - 16x - 16 + 8a - {a^2} = 0 $$ имеет не менее трёх корней.

$0 < a \le 4$

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10114.

19. Конечная возрастающая последовательность ${a_1}$, ${a_2}$, ... , ${a_n}$, состоит из n $ \ge $ 3 различных натуральных чисел, причём при всех натуральных $ k \le n - 2 $ выполнено равенство $ 5{a_{k + 2}} = 6{a_{k + 1}} - {a_k} $.
а) Приведите пример такой последовательности при $ n $ = 5.
б) Может ли в такой последовательности при некотором $n$ $ \ge $ 3 выполняться равенство $ 4{a_n} = 5{a_2} - {a_1} $ ?
в) Какое наименьшее значение может принимать ${a_1}$, если ${a_n}$ = 286?

а) например, последовательность 1, 126, 151, 156, 157
б) нет
в) 4

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10400.

Интеллектуальный и эстетичный кабинет для подготовки к ЕГЭ

Часть 2