Тест ЕГЭ по профильной математике решать онлайн

1. В треугольнике ABC угол C равен 90°, AB = 12, \( tgA = \frac{5}{ \sqrt {20}} \). Найдите AC.

Верный ответ: 8

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10444.

2. Даны векторы \( \vec a \)(4; -6) и \( \vec b \)(-2; 3). Известно, что \( \left| {\vec c} \right| = \left| {\vec a} \right| \), а векторы \( \vec c({x_c};{y_c}) \) и \( {\vec b} \) противоположно направленные. Найдите \( {x_c} + {y_c} \) .

Верный ответ: -2

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21358.

3. В сосуде, имеющем форму конуса, уровень жидкости достигает \( \frac{1}{2} \) высоты. Объём жидкости равен 54 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

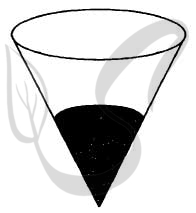
Верный ответ: 378

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10389.

4. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 7. Результат округлите до тысячных.

Верный ответ: 0,167

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10461.

5. В ящике 14 красных и 12 синих фломастеров. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый раз синий фломастер появится третьим по счету?

Верный ответ: 0,14

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 15374.

6. Найдите корень уравнения \( \sqrt {1 - 6x} = 7 \).

Верный ответ: -8

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10348.

7. Найдите \( \sin \alpha \), если \( \cos \alpha = \frac{{\sqrt 7 }}{4} \) и \( \alpha \in (\pi ;2\pi ) \).

Верный ответ: -0,75

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10219.

8. На рисунке изображён график \( y = f'(x) \) - производной функции \( f(x) \), определённой на интервале \( (-9; 4) \). Найдите точку экстремума функции \( f(x) \), принадлежащую отрезку \( [-5; 3] \).

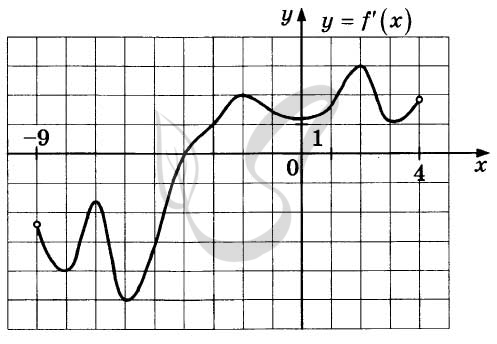
Верный ответ: -4

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10103.

9. Зависимость объёма спроса \( q \) (единиц в месяц) на продукцию предприятия-монополиста от цены \( p \) (тыс. руб. за ед.) задаётся формулой \( q=110-5p \). Выручка предприятия \(r \) (в тыс. руб. за месяц) вычисляется по формуле \( r(p)=q⋅p \). Определите наибольшую цену \( p \), при которой месячная выручка \( r(p) \) составит не менее 600 тыс. руб. Ответ приведите в тыс. руб. за ед.

Верный ответ: 12

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10505.

10. Первая труба пропускает на 3 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объёмом 594 литра она заполняет на 5 минут быстрее, чем первая труба заполняет резервуар объёмом 648 литров?

Верный ответ: 27

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10107.

11. На рисунке изображён график функции \( f\left( x \right) = b + {\log _a}x \). Найдите \( f\left( {\frac{1}{3}} \right) \).

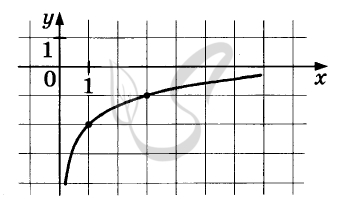
Верный ответ: -3

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 15373.

12. Найдите точку минимума функции \( y = (3 - 2x)\cos x + 2\sin x + 4 \), принадлежащую промежутку \( \left( {0;\frac{\pi }{2}} \right) \).

Верный ответ: 1,5

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10184.

Часть 2

13. Выполните следующие пункты:

а) Решите уравнение \( \left( {4~{{\sin }^2}x - 1} \right)\sqrt {{x^2} - 64{\pi ^2}} = 0 \).
б) Найдите все корни этого уравнения, принадлежащие отрезку \( \left[ 25;30 \right] \).

а) \( \pm 8\pi , - \frac{{47\pi }}{6} - \pi n; - \frac{{43\pi }}{6} - \pi n; \) \( \frac{{43\pi }}{6} + \pi n;\frac{{47\pi }}{6} + \pi n,n \in N \) ;

б) \( 8\pi ;\frac{{49\pi }}{6};\frac{{53\pi }}{6};\frac{{55\pi }}{6} \)

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10147.

14. В правильной четырёхугольной пирамиде SABCD с вершиной S сторона основания равна 8. Точка L - середина ребра SC. Тангенс угла между прямыми BL и SA равен \( 2\sqrt {\frac{2}{5}} \).
а) Пусть O - центр основания пирамиды. Докажите, что прямые BO и LO перпендикулярны.
б) Найдите площадь поверхности пирамиды.

б) 192

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10262.

15. Решите неравенство \( {\log _{\sqrt[4]{{25}}}}\left( {{{\log }_{\frac{1}{2}}}\left( {x + 2} \right)} \right) \ge 2 \).

\( - 2 < x \le - \frac{{63}}{{32}} \)

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10491.

16. Планируется выдать льготный кредит на целое число миллионов рублей на пять лет. В середине каждого года действия кредита долг заёмщика возрастает на 20% по сравнению с началом года. В конце 1-го, 2-го и 3-го годов заемщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наибольший размер кредита, при котором общая сумма выплат заёмщика будет меньше 10 млн руб.

5 млн рублей

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10132.

17. Прямая, проходящая через середину M гипотенузы AB прямоугольного треугольника ABC, перпендикулярна CM и пересекает катет AC в точке K. При этом AK : KC = 1 : 2.
а) Докажите, что \( \angle \)ВАС = 30°.
б) Пусть прямые MK и BC пересекаются в точке P, а прямые AP и BK - в точке Q. Найдите KQ, если BC = \( 3\sqrt 2 \).

б) \( 2\sqrt {42} \)

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10397.

18. Найдите все значения \(a \), при каждом из которых уравнение \( a{x^2} + 2(a + 2)x + (a + 5) = 0 \) имеет два корня, расстояние между которыми больше 1.

\( - 2 - 2\sqrt 5 < a < 0 \) ; \( 0 < a < 2\sqrt 5 - 2 \)

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10190.

19. На доске было написано 20 натуральных чисел (необязательно различных), каждое из которых не превосходит 40. Вместо некоторых из чисел (возможно, одного) на доске написали числа, меньшие первоначальных на единицу. Числа, которые после этого оказались равными 0, с доски стёрли.
а) Могло ли оказаться так, что среднее арифметическое чисел на доске увеличилось?
б) Среднее арифметическое первоначально написанных чисел равнялось 27. Могло ли среднее арифметическое оставшихся на доске чисел оказаться равным 34?
в) Среднее арифметическое первоначально написанных чисел равнялось 27. Найдите наибольшее возможное значение среднего арифметического чисел, которые остались на доске.

а) да
б) нет
в) \( 38\frac{1}{7} \)

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10267.

Интеллектуальный и эстетичный кабинет для подготовки к ЕГЭ

Часть 2