Тест ЕГЭ по профильной математике решать онлайн

1. В треугольнике со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведённая к первой из этих сторон, равна 4. Чему равна высота, проведённая ко второй стороне?

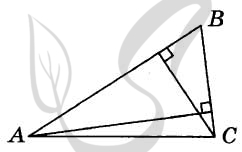
Верный ответ: 6

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10159.

2. На координатной плоскости изображены векторы $ \vec a $ и $ \vec b $. Найдите скалярное произведение $ \vec a \cdot \vec b $.

Верный ответ: 66

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21359.

3. Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).

Верный ответ: 18

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10370.

4. Одиннадцать детей встают в хоровод в случайном порядке. Среди них Антон и его сестра Маша. Какова вероятность того, что Антон и Маша окажутся рядом?

Верный ответ: 0,2

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10499.

5. В ящике 13 красных и 13 синих фломастеров. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый раз синий фломастер появится третьим по счету?

Верный ответ: 0,13

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 15376.

6. Найдите корень уравнения $ \sqrt {2x + 31} = 9 $.

Верный ответ: 25

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10291.

7. Найдите значение выражения $ \frac{{6\cos 207^\circ }}{{\cos 27^\circ }} $.

Верный ответ: -6

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10352.

8. На рисунке изображён график $ y = f'(x) $ - производной функции $ f(x) $, определённой на интервале (-4; 10). Найдите количество точек, в которых касательная к графику функции $ f(x) $ параллельна прямой $ y = - 2x + 16 $ или совпадает с ней.

Верный ответ: 4

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10369.

9. Наблюдатель, находящийся на высоте $ h $ м над поверхностью земли, видит линию горизонта на расстоянии $ l $ км, которое можно найти по формуле $ l = \sqrt {\frac{{Rh}}{{500}}} $‚ где $ R $ = 6400 км - радиус Земли.
Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 километра. К пляжу ведет лестница, каждая ступенька которой имеет высоту 20 см. На сколько ступенек ему нужно подняться, чтобы он увидел горизонт на расстоянии 9,6 километра?

Верный ответ: 27

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10467.

10. Первая труба наполняет бак объёмом 600 литров, а вторая труба - бак объёмом 900 литров. Известно, что одна из труб пропускает в минуту на 3 л воды больше, чем другая. Сколько литров воды в минуту пропускает вторая труба, если баки были наполнены за одно и то же время?

Верный ответ: 9

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10335.

11. На рисунке изображён график функции $ f\left( x \right) = b + {\log _a}x $. Найдите $ f\left( {\frac{1}{9}} \right) $.

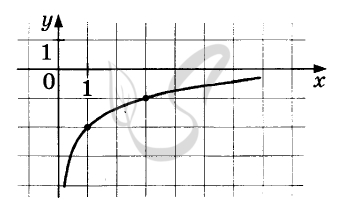
Верный ответ: -4

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 15375.

12. Найдите точку максимума функции $ y = - \frac{x}{{{x^2} + 121}} $.

Верный ответ: -11

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10431.

Часть 2

13. Выполните следующие пункты:

а) Решите уравнение $ 19 \cdot {4^x} - 5 \cdot {2^{x + 2}} + 1 = 0 $.
б) Найдите все корни этого уравнения, принадлежащие отрезку [-5; -4].

а) $ 0;-{\log _2}19 $

б) $ - {\log _2}19 $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10299.

14. На ребре AA₁ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ взята точка E так, что A₁E : EA = 3 : 2, на ребре BB₁ - точка F так, что B₁F : FB = 2 : 3, а на ребре B₁C₁ - точка T так, что B₁T : TC₁ = 2 : 1. Известно, что AB = 4, AD = 3, AA₁ = 5.
а) Докажите, что плоскость EFT проходит через вершину D₁.
б) Найдите угол между плоскостью EFT и плоскостью BB₁C₁.

б) $ \arccos \frac{1}{{\sqrt {33} }} $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10414.

15. Решите неравенство $ \sqrt[3]{{{8^{5x + 3}}}} < \sqrt {{{\left( {\frac{1}{{16}}} \right)}^{\frac{{2x + 1}}{x}}}} $.

$ x < - 1, - \frac{2}{5} < x < 0 $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10415.

16. 31 декабря 2016 года Василий взял в банке 5 460 000 рублей в кредит под 20% годовых. Схема выплаты кредита следующая - 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), затем Василий переводит в банк $ x $ рублей. Каким должно быть число $ x $, чтобы Василий выплатил долг тремя равными платежами (то есть за три года)?

2 592 000 рублей

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10493.

17. Медианы AA₁, BB₁ и CC₁, треугольника ABC пересекаются в точке M. Точки A₂, B₂ и C₂ - середины отрезков MA, MB и MC соответственно.
а) Докажите, что площадь шестиугольника A₁B₂C₁A₂B₁C₂ вдвое меньше площади треугольника ABC.
б) Найдите сумму квадратов всех сторон этого шестиугольника, если известно, что AB = 5, BC = 8 и AC = 10.

б) $ \frac{{63}}{2} $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10378.

18. Найдите все значения $a $, при каждом из которых система $$ \left\{ \begin{array}{l} \left| {2{x^2} + {y^2} - 1} \right| + {y^2} + 4y = 0 \\ y = 0,5x + a \end{array} \right. $$ имеет два или три корня.

$ \left( { - 1 - \frac{{\sqrt {30} }}{4}; - \frac{3}{8}} \right];\left[ { - \frac{{\sqrt 2 }}{4};\frac{{\sqrt 2 }}{4}} \right) $

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10285.

19. Ответьте на следующие вопросы:
а) Существует ли такое кратное 11 трёхзначное число, у которого вторая цифра в 14 раз меньше произведения двух других его цифр?
б) Существует ли такое кратное 11 трёхзначное число, у которого сумма всех цифр равна 1?
в) Найдите наибольшее кратное 11 восьмизначное число, среди цифр которого по одному разу встречаются цифры 1, 2, 3, 4, 5, 6, 7 и 9. Ответ обоснуйте.

а) да, например 847
б) нет
в) 97 635 241

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 10172.

Интеллектуальный и эстетичный кабинет для подготовки к ЕГЭ

Часть 2