


1. Согласно законам равноускоренного прямолинейного движения
\( s = {\upsilon _0}t + \frac{{a{t^2}}}{2} \) (1)
\( 4{\upsilon _0} = {\upsilon _0} + at \) (2)
где \( {\upsilon _0} \) — начальная скорость тела, \( a \) — модуль ускорения тела, \( s \) — путь,
пройденный телом.
2. Решая уравнения (1) и (2), получим выражение для начальной скорости тела:
\( {\upsilon _0} = \frac{s}{{2t}} = \frac{{20}}{{2 \cdot 2}} \) = 5 м/с
Ответ: \( {\upsilon _0} \) = 5 м/с
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21512.
1. Согласно законам равноускоренного прямолинейного движения
\( s = {\upsilon _0}t + \frac{{a{t^2}}}{2} \) (1)
\( 4{\upsilon _0} = {\upsilon _0} + at \) (2)
где \( {\upsilon _0} \) — начальная скорость тела, \( a \) — модуль ускорения тела, \( s \) — путь,
пройденный телом.
2. Решая уравнения (1) и (2), получим выражение для пути, пройденного телом:
\( s = \frac{{5{\upsilon _0}t}}{2} = \)\( \frac{{5 \cdot 3 \cdot 2}}{2} \) = 15 м
Ответ: s = 15 м
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21505.
1. Модуль ускорения поезда на всём пути является постоянной величиной и равен
\( a = \frac{{{\upsilon ^2}}}{{2s}} \) (1),
где \( \upsilon \) — скорость поезда в начале последнего километра пути, а \( s \) = 1 км — длина
этого участка пути
2. Модуль изменения скорости на этом участке пути равен
\( \Delta \upsilon = \upsilon = at \) (2)
3. Решая уравнения (1) и (2), получим выражение для времени прохождения поездом
последнего километра пути:
\( t = \frac{{2s}}{\upsilon } = \) \( \frac{{2 \cdot 1000}}{{10}} \) = 200 с
Ответ: t = 200 с
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21498.
1. Модуль ускорения поезда на всём пути является постоянной величиной и равен
\( a = \frac{{{\upsilon ^2}}}{{2s}} \) (1),
где \( \upsilon \) — скорость поезда в начале последнего километра пути, а \( s \) = 1 км — длина
этого участка пути
2. Модуль изменения скорости на этом участке пути равен
\( \Delta \upsilon = \upsilon = at \) (2)
3. Решая уравнения (1) и (2), получим выражение для скорости поезда в начале
последнего километра пути:
\( \upsilon = \frac{{2s}}{t} = \) \( \frac{{2 \cdot 1000}}{{250}} \) = 8 м/с
Ответ: \( \upsilon \) = 8 м/с
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21491.
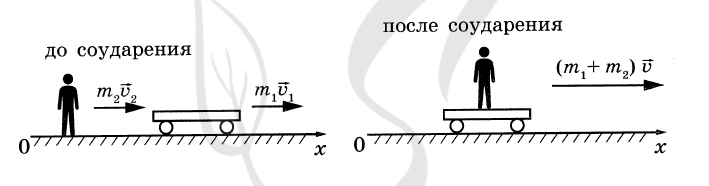
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21484.
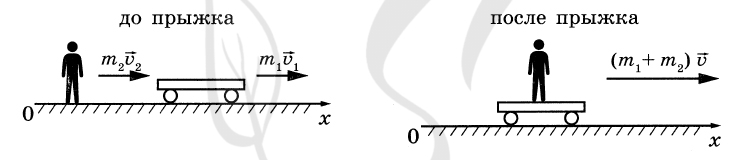
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21476.
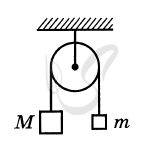
Запишем для двух грузов второй закон Ньютона в проекциях на вертикальную
ось:
\( M{a_1} = Mg - {T_1} \) ; \( m{a_2} = {T_2} - mg \)
Так как нить невесома и нерастяжима, а блок идеальный, то
\( {a_1} = {a_2} = a \) ; \( {T_1} = {T_2} = T \)
Для скорости, которую приобрёл правый груз, можно записать соотношение \( \upsilon = at \)
Тогда для силы натяжения нити получим:
\( T = m\left( {\frac{\upsilon }{t} + g} \right) = \)\( 1 \cdot \left( {\frac{4}{1} + 10} \right) \) = 14 Н
Ответ: T = 14 Н
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21468.
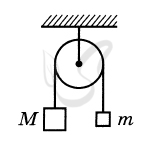
Запишем для двух грузов второй закон Ньютона в проекциях на вертикальную
ось:
\( M{a_1} = Mg - {T_1} \) ; \( m{a_2} = {T_2} - mg \)
Так как нить невесома и нерастяжима, а блок идеальный, то
\( {a_1} = {a_2} = a \) ; \( {T_1} = {T_2} = T \)
Для пути, который прошёл левый груз, можно записать соотношение:
\( S = \frac{{{\upsilon ^2}}}{{2a}} \)
Тогда для силы натяжения нити получим:
\( T = m\left( {\frac{{{\upsilon ^2}}}{{2S}} + g} \right) = \)\( 1\left( {\frac{{{4^2}}}{{2 \cdot 2}} + 10} \right) \) = 14 Н
Ответ: T = 14 Н
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21460.

Скорость тела определяется изменением его координаты с течением времени.
Анализируя график зависимости координаты автомобиля от времени \( x(t) \), видим,
что в промежутке от 4 до 5 мин его координата изменяется линейно и быстрее
всего. Следовательно, в этот промежуток времени автомобиль движется равномерно
с максимальной скоростью. Определим модуль максимальной скорости автомобиля:
\( {\upsilon _{\max }} = \frac{{\left| {x(5) - x(4)} \right|}}{{\Delta t}} = \)\( \frac{{\left| {300 - 900} \right|}}{{60}} \) = 10 м/с
Таким образом, максимальная кинетическая энергия автомобиля равна
\( {E_{k\max }} = \frac{{m\upsilon _{\max }^2}}{2} = \)\( \frac{{1700 \cdot {{10}^2}}}{2} \) = 85 · 103 Дж = 85 кДж
Ответ: \( {E_{k\max }} \) = 85 кДж
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21452.
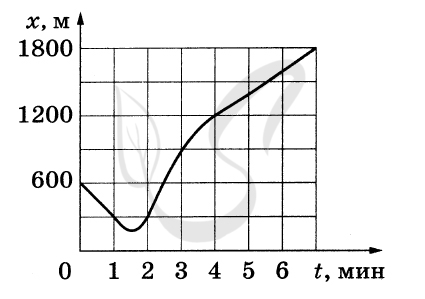
Скорость тела определяется изменением его координаты с течением времени.
Анализируя график зависимости координаты автомобиля от времени \( x(t) \), видим,
что в промежутке от 2 до 3 мин его координата изменяется линейно и быстрее
всего. Следовательно, в этот промежуток времени автомобиль движется равномерно
с максимальной скоростью. Определим модуль максимальной скорости автомобиля:
\( {\upsilon _{\max }} = \frac{{x(3) - x(2)}}{{\Delta t}} \)\( = \frac{{900 - 300}}{{60}} \) = 10 м/с
Таким образом, максимальная кинетическая энергия автомобиля равна
\( {E_{k\max }} = \frac{{m\upsilon _{\max }^2}}{2} \)\( = \frac{{2500 \cdot {{10}^2}}}{2} = \) 125 · 103 Дж = 125 кДж
Ответ: \( {E_{k\max }} \) = 125 кДж
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21444.