Линия заданий 22, ЕГЭ по физике

1. Поскольку нить, связывающая грузы, нерастяжима, то оба груза движутся с одинаковым ускорением, т. е. \( \left| {{{\vec a}_1}} \right| = \left| {{{\vec a}_2}} \right| = a \).
Поскольку эта нить невесома, модули сил натяжения нити, действующих на грузы, одинаковы, т. е. \( \left| {{{\vec T}_1}} \right| = \left| {{{\vec T}_2}} \right| = T \).

2. Рассмотрим случай, когда \( F \) = 18 Н, а \( T \) = 10 Н.

Запишем второй закон Ньютона для грузов в проекциях на горизонтальную ось Ох: для первого тела: \( F - T = {M_1}a \), для второго тела: \( T = {M_2}a \)

В итоге получим: \( {M_2} = \frac{T}{a} = \frac{{{M_1}T}}{{F - T}} \)\( = \frac{{2 \cdot 10}}{{18 - 10}} = 2,5 \) кг

Ответ: M₂ = 2,5 кг

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21436.

1. Поскольку нить, связывающая грузы, нерастяжима, то оба груза движутся с одинаковым ускорением, т. е. \( \left| {{{\vec a}_1}} \right| = \left| {{{\vec a}_2}} \right| = a \).
Поскольку эта нить невесома, модули сил натяжения нити, действующих на грузы, одинаковы, т. е. \( \left| {{{\vec T}_1}} \right| = \left| {{{\vec T}_2}} \right| = T \).

2. Рассмотрим случай, когда \( F \) = 18 Н, а \( T \) = 10 Н.

Запишем второй закон Ньютона для грузов в проекциях на горизонтальную ось Ох: для первого тела: \( F - T = {M_1}a \), для второго тела: \( T = {M_2}a \)

В итоге получим: \( {M_1} = \frac{{F - T}}{a} = \frac{{(F - T){M_2}}}{T} \)\( = \frac{{(18 - 10) \cdot 3}}{{10}} = 2,4 \) кг

Ответ: M₁ = 2,4 кг

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21428.

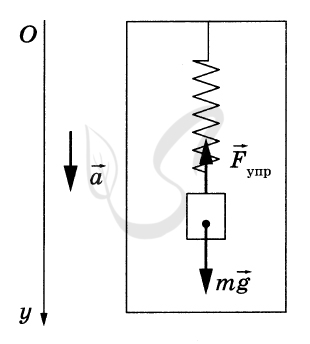
1. Выберем инерциальную систему отсчёта «шахта лифта», направив вертикальную ось \( Oy \) вниз по ускорению и расставив силы, действующие на груз, как показано на рисунке.

2. Запишем II закон Ньютона для груза в выбранной ИСО в проекциях на ось \( Oy \):

\( Oy:mg - {F_{упр}} = ma \)

откуда \( a = g - \frac{{{F_{упр}}}}{m} \). (2)

3. По закону Гука модуль силы упругости: \( {F_{упр}} = k\Delta y \), (3)
где \( k \) — жёсткость, а \( \Delta y \) — заданное удлинение пружины.

4. Подставив (3) в (2), находим проекцию искомого ускорения:

\( k = \frac{{m(g - a)}}{{\Delta y}} \)\( = \frac{{0,2 \cdot (10 - 2)}}{{0,01}} \) = 160 Н/м

Ответ: k = 160 Н/м

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21420.

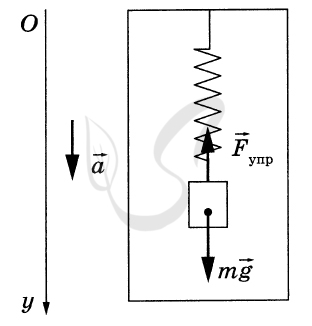
1. Выберем инерциальную систему отсчёта «шахта лифта», направив вертикальную ось \( Oy \) вниз по ускорению и расставив силы, действующие на груз, как показано на рисунке.

2. Запишем II закон Ньютона для груза в выбранной ИСО в проекциях на ось \( Oy \):

\( Oy:mg - {F_{упр}} = ma \)

откуда \( a = g - \frac{{{F_{упр}}}}{m} \). (2)

3. По закону Гука модуль силы упругости: \( {F_{упр}} = k\Delta y \), (3)
где \( k \) — жёсткость, а \( \Delta y \) — заданное удлинение пружины.

4. Подставив (3) в (2), находим проекцию искомого ускорения:

\( a = g - \frac{{k\Delta y}}{m} \)\( = 10 - \frac{{100 \cdot 0,015}}{{0,2}} \) = 2,5 м/с²

Ответ: a = 2,5 м/с²

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21412.

1. Шарики испытывают абсолютно неупругое соударение. Для системы из двух шариков в инерциальной системе отсчёта выполняется закон сохранения импульса (ЗСИ), так как при малом времени взаимодействия действием внешней силы (силы тяжести) можно пренебречь.

2. Взаимодействие шаров можно изобразить так, как показано на рисунке.

3. С учётом того, что \( \left| {{{\vec \upsilon }_1}} \right| = \left| {{{\vec \upsilon }_2}} \right| = {\upsilon _2} \), а совместная скорость после соударения равна \( u \), запишем ЗСИ в проекциях на ось \( Ox \):

\( 3m\upsilon - m\upsilon = 4m\upsilon \), откуда \( u = \upsilon /2 = 4/2 = 2 \) = 2 м/с

Ответ: \( u \) = 2 м/с

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21404.

1. Шарики испытывают абсолютно неупругое соударение. Для системы из двух шариков в инерциальной системе отсчёта выполняется закон сохранения импульса (ЗСИ), так как при малом времени взаимодействия действием внешней силы (силы тяжести) можно пренебречь.

2. Взаимодействие шаров можно изобразить так, как показано на рисунке.

3. С учётом того, что \( \left| {{{\vec \upsilon }_1}} \right| = \left| {{{\vec \upsilon }_2}} \right| = {\upsilon _2} \), а совместная скорость после соударения равна \( u \), запишем ЗСИ в проекциях на ось \( Ox \):

\( 3m\upsilon - m\upsilon = 4m\upsilon \), откуда \( \upsilon = 2u = 2 \cdot 0,5 \) = 1 м/с

Ответ: \( \upsilon \) = 1 м/с

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21396.

1. Так как после достижения теплового равновесия в воде всё ещё плавает лёд, то это означает, что конечная температура, установившаяся в калориметре, 0 °С.

2. Так как потери по условию отсутствуют, то всё количество теплоты, отданное водой при охлаждении от 15 до 0 °С, пошло на плавление льда, имевшего температуру плавления. Запишем уравнение теплового баланса:

\( \left| {{Q_{отд}}} \right| = \left| {{Q_{пол}}} \right| \) или \( c{m_{вод}}({t_{гор}} - {t_{хол}}) = \lambda {m_{лед}} \),

откуда \( {m_{вод}} = \frac{{\lambda {m_{лед}}}}{{c({t_{гор}} - {t_{хол}})}} \), (1)

где \( c \) и \( {{m_{вод}}} \) — удельная теплоёмкость и масса воды соответственно, \( \lambda \) и \( {{m_{лед}}} \) — удельная теплота плавления и масса растаявшего льда, \( {{t_{гор}}} \) и \( {{t_{хол}}} \) — начальная и конечная температура воды.

3. Подставив числовые значения в (1), получим искомую величину:

\( {m_{вод}} = \frac{{330 \cdot {{10}^3} \cdot 0,12}}{{4,2 \cdot {{10}^3} \cdot (15 - 0)}} \) ≈ 0,63 кг = 630 г

Ответ: m_воды = 630 г.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21388.

1. Так как после достижения теплового равновесия в воде всё ещё плавает лёд, то это означает, что конечная температура, установившаяся в калориметре, 0 °С.

2. Так как потери по условию отсутствуют, то всё количество теплоты, отданное водой при охлаждении от 15 до 0 °С, пошло на плавление льда, имевшего температуру плавления. Запишем уравнение теплового баланса:

\( \left| {{Q_{отд}}} \right| = \left| {{Q_{пол}}} \right| \) или \( c{m_{вод}}({t_{гор}} - {t_{хол}}) = \lambda {m_{лед}} \),

откуда \( {m_{лед}} = \frac{{c{m_{вод}}({t_{гор}} - {t_{хол}})}}{\lambda } \), (1)

где \( c \) и \( {{m_{вод}}} \) — удельная теплоёмкость и масса воды соответственно, \( \lambda \) и \( {{m_{лед}}} \) — удельная теплота плавления и масса растаявшего льда, \( {{t_{гор}}} \) и \( {{t_{хол}}} \) — начальная и конечная температура воды.

3. Подставив числовые значения в (1), получим искомую величину:

\( {m_{лед}} = \frac{{4,2 \cdot {{10}^3} \cdot 1,1 \cdot (15 - 0)}}{{330 \cdot {{10}^3}}} \)\( = 0,21 \) кг = 210 г

Ответ: m_льда = 210 г.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21380.

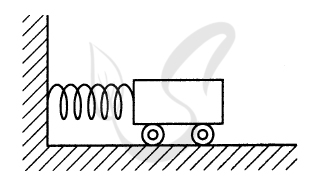
В случае гармонических колебаний максимальная потенциальная энергия пружины равна максимальной кинетической энергии тележки: \( \frac{{k{A^2}}}{2} = \frac{{m{\upsilon ^2}}}{2} \)‚ где k - жёсткость пружины, A - амплитуда колебаний тележки, m - масса тележки, \( \upsilon \) - максимальная скорость тележки.

В итоге получим: \( \upsilon = A\sqrt {\frac{k}{m}} \) = \( 0,1\sqrt {\frac{{200}}{2}} \) = 1 м/с

Ответ: \( \upsilon \) = 1 м/с

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21372.

В случае гармонических колебаний максимальная потенциальная энергия пружины равна максимальной кинетической энергии тележки: \( \frac{{k{A^2}}}{2} = \frac{{m{\upsilon ^2}}}{2} \)‚ где k - жёсткость пружины, A - амплитуда колебаний тележки, m - масса тележки, \( \upsilon \) - максимальная скорость тележки.

В итоге получим: А = \( \upsilon \sqrt {\frac{m}{k}} = 3 \cdot \sqrt {\frac{{0,5}}{{200}}} \) = 0,15 м

Ответ: А = 0,15 м.

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21364.