Линия заданий 23, ЕГЭ по физике

Так как в калориметре лёд и вода находятся в тепловом равновесии, то температура смеси равна 0 °С. При опускании в смесь болта в теплообмене будут участвовать лёд и болт. При минимальной удельной теплоёмкости материала болта он охладится до 0 °С. Уравнение теплового баланса: \( c{m_1}({t_1} - 0^\circ C) = \lambda {m_2} \).

Для минимальной удельной теплоёмкости болта получим:

\( c = \frac{{\lambda {m_2}}}{{{m_1}{t_1}}} = \)\( \frac{{3,3 \cdot {{10}^5} \cdot 5 \cdot {{10}^{ - 3}}}}{{50 \cdot {{10}^{ - 3}} \cdot 66}} \) = 500 \( \frac{{Дж}}{{кг}} \cdot C^\circ \)

Ответ: \( c \) = 500 \( \frac{{Дж}}{{кг}} \cdot C^\circ \)

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21513.

Так как в калориметре лёд и вода находятся в тепловом равновесии, то температура смеси равна 0 °С. При опускании в смесь болта в теплообмене будут участвовать лёд и болт. При минимальной удельной теплоёмкости материала болта он охладится до 0 °С. Уравнение теплового баланса: \( c{m_1}({t_1} - 0^\circ C) = \lambda {m_2} \).

Для массы болта получим:

\( {m_1} = \frac{{\lambda {m_2}}}{{c{t_1}}} = \) \( \frac{{3,3 \cdot {{10}^5} \cdot 5 \cdot {{10}^{ - 3}}}}{{500 \cdot 66}} \) = 0,05 кг

Ответ: m₁ = 0,05 кг

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21506.

Согласно первому закону термодинамики количество теплоты, полученное газом, \( Q = \Delta U + A \), где \( \Delta U = \frac{3}{2}\nu R\Delta T = \frac{3}{2}p\Delta V \)— изменение внутренней энергии газа в изобарном процессе, \( A = p\Delta U \) — работа газа. Таким образом,

\( Q = \frac{3}{2}p\Delta V + p\Delta V \) = \( \frac{5}{2}p\Delta V = \frac{5}{3}\Delta U = \frac{{5 \cdot 1800}}{3} \) = 3000 кДж

Ответ: \( Q \) = 3000 кДж

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21499.

Согласно первому закону термодинамики количество теплоты, полученное газом, \( Q = \Delta U + A \), где \( \Delta U = \frac{3}{2}\nu R\Delta T = \frac{3}{2}p\Delta V \)— изменение внутренней энергии газа в изобарном процессе, \( A = p\Delta U \) — работа газа. Таким образом,

\( Q = \frac{3}{2}p\Delta V + p\Delta V = \frac{5}{2}p\Delta V \)\( = \frac{5}{2}A = \frac{{5 \cdot 1600}}{2} \) = 4 кДж

Ответ: \( Q \) = 4 кДж

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21492.

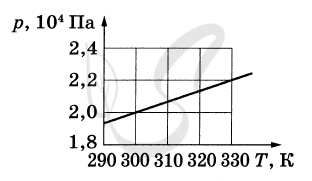
Из уравнения Менделеева-Клапейрона \( pV = \nu RT \) определим количество вещества:

\( \nu = \frac{{pV}}{{RT}} \)

Из графика при давлении \( p = 2 \cdot {10^4} \) Па температура газа \( T \) = 300 К. Отсюда:

\( \nu = \frac{{2 \cdot {{10}^4} \cdot 0,25}}{{8,31 \cdot 300}} \) ≈ 2 моль

Ответ: \( \nu \) ≈ 2 моль

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21485.

Из уравнения Менделеева-Клапейрона \( pV = \nu RT \) определим объём:

\( V = \frac{{\nu RT}}{p} \)

Из графика при давлении \( p = 2 \cdot {10^4} \) Па температура газа \( T \) = 300 К. Отсюда:

\( V = \frac{{3 \cdot 8,31 \cdot 300}}{{2 \cdot {{10}^4}}} \) ≈ 0,37 м³

Ответ: V ≈ 0,37 м³

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21477.

В теплообмене участвуют лёд и вода. Так как лёд тающий, то его начальная температура равна 0 °С. В момент, когда кусочки льда перестают таять, вода охлаждается до температуры плавления льда и, следовательно, температура смеси становится равной 0 °С.

Уравнение теплового баланса: \( c{m_1}({t_1} - 0^\circ C) = \lambda {m_2} \)

Для массы воды получим:

\( {m_1} = \frac{{\lambda {m_2}}}{{c{t_1}}} = \)\( \frac{{3,3 \cdot {{10}^5} \cdot 140 \cdot {{10}^{ - 3}}}}{{4200 \cdot 20}} \) = 0,55 кг

Ответ: \( {m_1} \) = 0,55 кг

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21469.

В теплообмене участвуют лёд и вода. Так как лёд тающий, то его начальная температура равна 0 °С. В момент, когда кусочки льда перестают таять, вода охлаждается до температуры плавления льда и, следовательно, температура смеси становится равной 0 °С.

Уравнение теплового баланса: \( c{m_1}({t_1} - 0^\circ C) = \lambda {m_2} \)

Для начальной температуры воды получим:

\( {t_1} = \frac{{\lambda {m_2}}}{{c{m_1}}} = \)\( \frac{{3,3 \cdot {{10}^5} \cdot 63 \cdot {{10}^{ - 3}}}}{{4200 \cdot 330 \cdot {{10}^{ - 3}}}} \) = 15 °С

Ответ: \( {t_1} \) = 15 °С

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21461.

Запишем формулу для рассеивающей линзы: \( - \frac{1}{F} = \frac{1}{d} - \frac{1}{f} \), где \( d \) — расстояние от предмета до линзы. В формуле учтено, что изображение предмета мнимое.

Из условия задачи следует, что \( \frac{d}{f} \) = 5.

Проведя преобразования, для модуля фокуса линзы получим: \( \left| F \right| = \frac{d}{4} = \frac{{20}}{4} \) = 5 см

Ответ: \( \left| F \right| \) = 5 см

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21453.

Запишем формулу для рассеивающей линзы: \( - \frac{1}{{\left| F \right|}} = \frac{1}{d} - \frac{1}{f} \), где \( d \) — расстояние от предмета до линзы. В формуле учтено, что изображение предмета мнимое.

Из условия задачи следует, что \( \frac{d}{f} \) = 4

Проведя преобразования, для модуля фокуса линзы получим: \( \left| F \right| = \frac{{4f}}{3} = \frac{{4 \cdot 9}}{3} \) = 12 см

Ответ: \( \left| F \right| \) = 12 см

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21445.