Линия заданий 24, ЕГЭ по физике

1. Определим степень изотермического сжатия, при которой пар станет насыщенным. При этом учтём, что при 100 °С давление насыщенного водяного пара равно нормальному атмосферному давлению \( {p_н} = {p_{атм}} = {10^5} \) Па. Для этого воспользуемся законом Бойля-Мариотта \( {p_{п1}}{V_1} = {p_н}{V_н} \). Поскольку начальная относительная влажность воздуха равна:

\( \varphi = \frac{{{p_{п1}}}}{{{p_н}}} = 0,6 \), то

\( \frac{{{V_1}}}{{{V_н}}} = \frac{{{p_н}}}{{{p_{п1}}}} = \)\( \frac{{{p_н}}}{{0,6{p_н}}} = \frac{{5}}{3} < 2,5 \)

Следовательно, при изотермическом уменьшении объёма в 2,5 раза пар станет насыщенным.

2. Определим начальное и конечное парциальное давление сухого воздуха, воспользовавшись законами Дальтона и Бойля-Мариотта:

\( {p_{в1}} = {p_1} - {p_{п1}} = {p_1} - \varphi {p_н} \) \( = {10^5} - 0,6 \cdot {10^5} = 0,4 \cdot {10^5} \) Па,

\( {p_{в2}} = \frac{{{p_{в1}}{V_1}}}{{{V_2}}} = \)\( 2,5 \cdot 0,4 \cdot {10^5} = {10^5} \) Па

3. Определим конечное давление влажного воздуха в сосуде с помощью закона Дальтона:

\( {p_2} = {p_{в2}} + {p_{п2}} = {p_{в2}} + {p_н} \) \( = {10^5} + {10^5} = 2 \cdot {10^5} \) Па.

4. При нагревании влажного воздуха без изменения объёма водяной пар будет оставаться ненасыщенным, а значит, влажный воздух можно считать идеальным газом с постоянным количеством вещества, для изохорного нагревания которого можно применить закон Шарля: \( \frac{{{p_1}}}{{{T_1}}} = \frac{{{p_2}}}{{{T_2}}} \). Таким образом, для того чтобы получить такое же конечное давление без изменения объёма, абсолютную температуру газа необходимо увеличить в

\( \frac{{{T_2}}}{{{T_1}}} = \frac{{{p_2}}}{{{p_1}}} = \frac{{2 \cdot {{10}^5}}}{{{{10}^5}}} = 2 \) раза

Ответ: \( \frac{{{T_2}}}{{{T_1}}} \) = 2

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21514.

1. Определим степень изотермического сжатия, при которой пар станет насыщенным. При этом учтём, что при 100 °С давление насыщенного водяного пара равно нормальному атмосферному давлению \( {p_н} = {p_{атм}} = {10^5} \) Па. Для этого воспользуемся законом Бойля-Мариотта \( {p_{п1}}{V_1} = {p_н}{V_н} \). Поскольку начальная относительная влажность воздуха равна:

\( \varphi = \frac{{{p_{п1}}}}{{{p_н}}} = 0,7 \), то

\( \frac{{{V_1}}}{{{V_н}}} = \frac{{{p_н}}}{{{p_{п1}}}} = \)\( \frac{{{p_н}}}{{0,7{p_н}}} = \frac{{10}}{7} < 3 \)

Следовательно, при изотермическом уменьшении объёма в 3 раза пар станет насыщенным.

2. Определим начальное и конечное парциальное давление сухого воздуха, воспользовавшись законами Дальтона и Бойля-Мариотта:

\( {p_{в1}} = {p_1} - {p_{п1}} = {p_1} - \varphi {p_н} \) \( = {10^5} - 0,7 \cdot {10^5} = 0,3 \cdot {10^5} \) Па,

\( {p_{в2}} = \frac{{{p_{в1}}{V_1}}}{{{V_2}}} = \)\( 3 \cdot 0,3 \cdot {10^5} = 0,9 \cdot {10^5} \) Па

3. Определим конечное давление влажного воздуха в сосуде с помощью закона Дальтона:

\( {p_2} = {p_{в2}} + {p_{п2}} = {p_{в2}} + {p_н} \) \( = {10^5} + 0,9 \cdot {10^5} = 1,9 \cdot {10^5} \) Па.

4. При нагревании влажного воздуха без изменения объёма водяной пар будет оставаться ненасыщенным, а значит, влажный воздух можно считать идеальным газом с постоянным количеством вещества, для изохорного нагревания которого можно применить закон Шарля: \( \frac{{{p_1}}}{{{T_1}}} = \frac{{{p_2}}}{{{T_2}}} \). Таким образом, для того чтобы получить такое же конечное давление без изменения объёма, абсолютную температуру газа необходимо увеличить до \( {T_2} = {T_1}\frac{{{p_2}}}{{{p_1}}} = \) \( 373 \cdot \frac{{1,9 \cdot {{10}^5}}}{{{{10}^5}}} \) ≈ 709 К

Ответ: T₂ ≈ 709 К

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21507.

1. Запишем в инерциальной системе отсчёта второй закон Ньютона для неподвижного поршня в неподвижном сосуде:

\( ({p_1} - {p_0})S - mg = 0 \)

где \( m \) — масса поршня, \( S \) — площадь его поперечного сечения, \( {p_0} \) — внешнее давление, \( {p_1} \) — давление газа под поршнем в покоящемся сосуде.

2. В проекциях на ось \( Ox \) второй закон Ньютона для поршня, неподвижного относительно сосуда, движущегося с ускорением \( \vec a:({p_2} - {p_0})S - mg = ma \), где \( {p_2} \) — давление газа в сосуде, движущемся с ускорением. При этом результирующая сила давления \( F = ({p_2} - {p_0})S \) (см. рисунок).

3. По закону Бойля-Мариотта для газа под поршнем имеем:

\( {p_1}{V_1} = {p_2}{V_2} \Rightarrow \) \( {p_1}S{h_1} = {p_2}S{h_2} \Rightarrow \) \( {p_1} = {p_2}(1 - \eta ) \),

где \( {h_1} \), \( {h_2} \) — начальная и конечная высота столба газа под поршнем соответственно, а \( \eta = \frac{{{h_1} - {h_2}}}{{{h_1}}} \) — относительное изменение высоты столба газа.

4. Решая систему уравнений

\( \left\{ \begin{array}{l} {p_1}S = {p_0}S + mg\\ {p_2}S = {p_0}S + mg + ma\\ {p_1} = {p_2}(1 - \eta ) \end{array} \right. \)

получим выражение для внешнего давления:

\( {p_0} = \frac{m}{{\eta S}}\left\{ {\left. {(1 - \eta )a - \eta g} \right\}} \right. \) = \( \frac{{10}}{{0,05 \cdot 50 \cdot {{10}^{ - 4}}}} \cdot (0,95 \cdot 1 - 0,05 \cdot 10) \) = 18 · 10³ Па = 18 кПа

Ответ: \( {p_0} \) = 18 · 10³ Па = 18 кПа

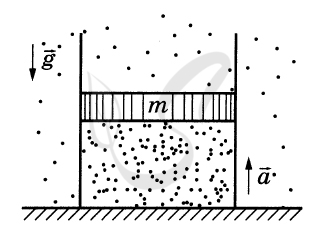
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21500.

1. Запишем в инерциальной системе отсчёта второй закон Ньютона для неподвижного поршня в неподвижном сосуде:

\( ({p_1} - {p_0})S - mg = 0 \)

где \( m \) — масса поршня, \( S \) — площадь его поперечного сечения, \( {p_0} \) — внешнее давление, \( {p_1} \) — давление газа под поршнем в покоящемся сосуде.

2. В проекциях на ось \( Ox \) второй закон Ньютона для поршня, неподвижного относительно сосуда, движущегося с ускорением \( \vec a:({p_2} - {p_0})S - mg = ma \), где \( {p_2} \) — давление газа в сосуде, движущемся с ускорением. При этом результирующая сила давления \( F = ({p_2} - {p_0})S \) (см. рисунок).

3. По закону Бойля-Мариотта для газа под поршнем имеем:

\( {p_1}{V_1} = {p_2}{V_2} \Rightarrow \) \( {p_1}S{h_1} = {p_2}S{h_2} \Rightarrow \) \( {p_1} = {p_2}(1 - \eta ) \),

где \( {h_1} \), \( {h_2} \) — начальная и конечная высота столба газа под поршнем соответственно, а \( \eta = \frac{{{h_1} - {h_2}}}{{{h_1}}} \) — относительное изменение высоты столба газа.

4. Решая систему уравнений

\( \left\{ \begin{array}{l} {p_1}S = {p_0}S + mg\\ {p_2}S = {p_0}S + mg + ma\\ {p_1} = {p_2}(1 - \eta ) \end{array} \right. \)

получим выражение для массы поршня:

\( m = \frac{{{p_0}\eta S}}{{(1 - \eta )a - \eta g}} \) \( = \frac{{28 \cdot {{10}^3} \cdot 0,05 \cdot 50 \cdot {{10}^{ - 4}}}}{{(1 - 0,05) \cdot 2 - 0,05 \cdot 10}} \) = 5 кг

Ответ: m = 5 кг

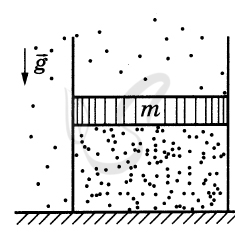
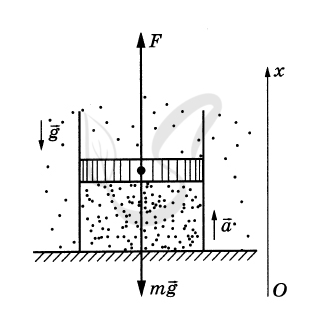
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21493.

1. Относительная влажность воздуха в трубке в первом случае: \( {\varphi _1} = \frac{{{p_1}}}{{{p_н}}} \), где \( {p_1} \) — давление водяных паров в трубке, \( {p_н} \) — давление насыщенных водяных паров при той же температуре. Для второго случая относительная влажность воздуха в трубке: \( {\varphi _2} = \frac{{{p_2}}}{{{p_н}}} \), где \( {{p_2}} \) — парциальное давление водяных паров в трубке.

2. Давление влажного воздуха в первом случае равно атмосферному давлению: \( {p_{1вл}} = {p_0} \), а во втором случае - \( {p_{2вл}} = {p_0} - \rho gl \), где \( \rho \) — плотность ртути, а \( l \) — длина столбика ртути. Заметим, что \( {p_0} = \rho gH \), где \( H \) = 760 мм.

3. Объём влажного воздуха при изменении положения трубки изменился так, как изменились длины столбиков воздуха, запертых ртутью. Считаем влажный воздух идеальным газом. Поэтому по закону Бойля-Мариотта можем записать

\( \frac{{{V_2}}}{{{V_1}}} = \frac{{{l_2}}}{{{l_1}}} = \)\( \frac{{{p_0}}}{{{p_0} - \rho gl}} \)

4. Из уравнения Менделеева-Клапейрона следует, что

\( p = \frac{{\nu RT}}{V} \), \( {p_{вл}} = \frac{{(\nu + {\nu _{св}})RT}}{V} \),

где \( p \) — парциальное давление водяного пара, \( {p_{вл}} \) — давление влажного воздуха, \( \nu \) — количество моль водяного пара в трубке, \( {{\nu _{св}}} \) — количество моль сухого воздуха в трубке.

Отсюда следует, что \( \frac{p}{{{p_{вл}}}} = \frac{\nu }{{\nu + {\nu _{св}}}} = const \)

Поэтому \( \frac{{{p_1}}}{{{p_2}}} = \frac{{{p_{1вл}}}}{{{p_{2вл}}}} \), и для изотермического процесса для парциальных давлений водяного пара имеем:

\( \frac{{{p_1}}}{{{p_2}}} = \frac{{{V_2}}}{{{V_1}}} = \frac{{{p_0}}}{{{p_0} - \rho gl}} \)

5. После объединения записанных выше уравнений получим выражение для относительной влажности воздуха во втором случае:

\( {\varphi _2} = {\varphi _1} \cdot \frac{{{p_0} - \rho gl}}{{{p_0}}} = \) \( {\varphi _1} \cdot \frac{{\rho gH - \rho gl}}{{\rho gH}} \)\( = {\varphi _1}\frac{{H - l}}{H} = \) \( 80 \cdot \frac{{760 - 76}}{{760}} \) = 72%

Ответ: \( {\varphi _2} \) = 72%

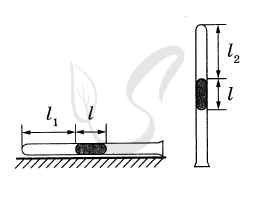
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21486.

1. Относительная влажность воздуха в трубке в первом случае: \( {\varphi _1} = \frac{{{p_1}}}{{{p_н}}} \), где \( {p_1} \) — давление водяных паров в трубке, \( {p_н} \) — давление насыщенных водяных паров при той же температуре. Для второго случая относительная влажность воздуха в трубке: \( {\varphi _2} = \frac{{{p_2}}}{{{p_н}}} \), где \( {{p_2}} \) — парциальное давление водяных паров в трубке.

2. Давление влажного воздуха в первом случае равно атмосферному давлению: \( {p_{1вл}} = {p_0} \), а во втором случае - \( {p_{2вл}} = {p_0} + \rho gl \), где \( \rho \) — плотность ртути, а \( l \) — длина столбика ртути. Заметим, что \( {p_0} = \rho gH \), где \( H \) = 760 мм.

3. Объём влажного воздуха при изменении положения трубки изменился так, как изменились длины столбиков воздуха, запертых ртутью. Считаем влажный воздух идеальным газом. Поэтому по закону Бойля-Мариотта можем записать

\( \frac{{{V_2}}}{{{V_1}}} = \frac{{{l_2}}}{{{l_1}}} = \)\( \frac{{{p_0}}}{{{p_0} + \rho gl}} \)

4. Из уравнения Менделеева-Клапейрона следует, что

\( p = \frac{{\nu RT}}{V} \), \( {p_{вл}} = \frac{{(\nu + {\nu _{св}})RT}}{V} \),

где \( p \) — парциальное давление водяного пара, \( {p_{вл}} \) — давление влажного воздуха, \( \nu \) — количество моль водяного пара в трубке, \( {{\nu _{св}}} \) — количество моль сухого воздуха в трубке.

Отсюда следует, что \( \frac{p}{{{p_{вл}}}} = \frac{\nu }{{\nu + {\nu _{св}}}} = const \)

Поэтому \( \frac{{{p_1}}}{{{p_2}}} = \frac{{{p_{1вл}}}}{{{p_{2вл}}}} \), и для изотермического процесса для парциальных давлений водяного пара имеем:

\( \frac{{{p_1}}}{{{p_2}}} = \frac{{{V_2}}}{{{V_1}}} = \frac{{{p_0}}}{{{p_0} + \rho gl}} \)

5. После объединения записанных выше уравнений получим выражение для относительной влажности воздуха во втором случае:

\( {\varphi _2} = {\varphi _1} \cdot \frac{{{p_0} + \rho gl}}{{{p_0}}} = \) \( {\varphi _1} \cdot \frac{{\rho gH + \rho gl}}{{\rho gH}} \)\( = {\varphi _1}\frac{{H + l}}{H} = \) \( 60 \cdot \frac{{760 + 100}}{{760}} \) = 68%

Ответ: \( {\varphi _2} \) = 68%

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21478.

1. Водяной пар в воздухе до момента конденсации является разреженным газом и описывается уравнением Менделеева — Клапейрона: \( pV = \frac{m}{M}RT \), где \( p \) — парциальное давление пара, \( m \) — масса пара в рассматриваемом объёме \( V \), \( T \) — абсолютная температура, а \( M \) = 18 · 10^-3 кг/моль — молярная масса воды

При комнатной температуре \( {T_1} \), и парциальном давлении \( {p_1} \) в выделенном объёме \( V \) содержится \( {m_1} = M\frac{{{p_1}V}}{{R{T_1}}} \) водяного пара, а в выдыхаемом воздухе при температуре \( {T_2} \) и парциальном давлении \( {p_2} \) содержится \( {m_2} = M\frac{{{p_2}V}}{{R{T_2}}} \)

2. Масса испарённой воды в этом объёме:

\( m = {m_2} - {m_1} = M\frac{{{p_2}V}}{{R{T_2}}} \)\( - M\frac{{{p_1}V}}{{R{T_1}}} = \frac{{MV}}{R}\left( {\frac{{{p_2}}}{{{T_2}}} - \frac{{{p_1}}}{{{T_1}}}} \right) \)

При \( {t_1} \) = 20 °С (\( {T_1} \) = 273 + 20 = 293 К) и относительной влажности 40 % парциальное давление водяного пара \( {p_1} = 0,4{p_{н1}} = 0,4 \cdot 2,34 \cdot {10^3} \) Па = 936 Па, а при \( {t_2} \) = 34 °С (\( {T_2} \) = 273 + 34 = 307 К) и относительной влажности 100 % парциальное давление водяного пара \( {p_2} = {p_{н2}} = 5320 \) Па

Здесь \( {p_{н1}} = 2,34 \cdot {10^3} \) Па — давление насыщенного водяного пара при \( {t_1} \) = 20 °С, а \( {p_{н2}} \) = 5320 Па — давление насыщенного водяного пара при \( {t_2} \) = 34 °С

3. Через лёгкие за 1 мин проходит 15 л воздуха, а за 1 ч. — 900 л, т.е. \( V \) = 0,9 м³. Подставляя значения физических величин, получим количество потерянной за час воды:

\( m = \frac{{MV}}{R}\left( {\frac{{{p_2}}}{{{T_2}}} - \frac{{{p_1}}}{{{T_1}}}} \right) = \)\( \frac{{18 \cdot {{10}^{ - 3}} \cdot 0,9}}{{8,31}} \cdot \left( {\frac{{5320}}{{307}} - \frac{{936}}{{293}}} \right) \) ≈ 27,6 · 10^-3 кг = 27,6 г

Ответ: m ≈ 27,6 г

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21470.

1. Водяной пар в воздухе до момента конденсации является разреженным газом и описывается уравнением Менделеева — Клапейрона: \( pV = \frac{m}{M}RT \), где \( p \) — парциальное давление пара, \( m \) — масса пара в рассматриваемом объёме \( V \), \( T \) — абсолютная температура, а \( M \) = 18 · 10^-3 кг/моль — молярная масса воды

При комнатной температуре \( {T_1} \), и парциальном давлении \( {p_1} \) в выделенном объёме \( V \) содержится \( {m_1} = M\frac{{{p_1}V}}{{R{T_1}}} \) водяного пара, а в выдыхаемом воздухе при температуре \( {T_2} \) и парциальном давлении \( {p_2} \) содержится \( {m_2} = M\frac{{{p_2}V}}{{R{T_2}}} \)

2. Масса испарённой воды в этом объёме:

\( m = {m_2} - {m_1} = M\frac{{{p_2}V}}{{R{T_2}}} \)\( - M\frac{{{p_1}V}}{{R{T_1}}} = \frac{{MV}}{R}\left( {\frac{{{p_2}}}{{{T_2}}} - \frac{{{p_1}}}{{{T_1}}}} \right) \)

При \( {t_1} \) = 17 °С (\( {T_1} \) = 273 + 17 = 290 К) и относительной влажности 40 % парциальное давление водяного пара \( {p_1} = 0,6{p_{н1}} = 0,6 \cdot 1,94 \cdot {10^3} \) Па = 1164 Па, а при \( {t_2} \) = 34 °С (\( {T_2} \) = 273 + 34 = 307 К) и относительной влажности 100 % парциальное давление водяного пара \( {p_2} = {p_{н2}} = 5320 \) Па

Здесь \( {p_{н1}} = 1,94 \cdot {10^3} \) Па — давление насыщенного водяного пара при \( {t_1} \) = 17 °С, а \( {p_{н2}} \) = 5320 Па — давление насыщенного водяного пара при \( {t_2} \) = 34 °С

3. Через лёгкие за 1 мин проходит 15 л воздуха, а за 20 мин. — 300 л, т.е. \( V \) = 0,3 м³. Подставляя значения физических величин, получим количество потерянной за час воды:

\( m = \frac{{MV}}{R}\left( {\frac{{{p_2}}}{{{T_2}}} - \frac{{{p_1}}}{{{T_1}}}} \right) = \)\( \frac{{18 \cdot {{10}^{ - 3}} \cdot 0,3}}{{8,31}} \cdot \left( {\frac{{5320}}{{307}} - \frac{{1164}}{{290}}} \right) \) ≈ 8,65 · 10^-3 кг = 8,65 г

Ответ: m ≈ 8,65 г

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21462.

1. Запишем уравнение Менделеева — Клапейрона для газа в верхней и нижней частях сосуда в начальном равновесном состоянии: \( {p_1}{V_1} = \nu RT \), \( {p_2}{V_2} = \nu RT \), где \( {p_1} \), \( {p_2} \) — давление воздуха в верхней и нижней частях сосуда, \( {V_1} \), \( {V_2} \) — объёмы верхней и нижней частей сосуда.

2. Запишем уравнение Менделеева Клапейрона для газа в верхней и нижней частях сосуда после откачки воздуха: \( {p_1}'{V_1}' = \nu RT \), \( {p_2}'{V_2}' = (\nu - \Delta \nu )RT \) где \( {p_1}' \), \( {p_2}' \) — давление воздуха в верхней и нижней частях сосуда, \( {V_1}' \), \( {V_2}' \) — объёмы верхней и нижней частей сосуда.

3. Условие механического равновесия поршня в начальном состоянии: \( {p_2} - {p_1} = \frac{{Mg}}{S} \), а после откачки воздуха: \( {p_2}' - {p_1}' = \frac{{Mg}}{S} \), где M — масса поршня, S — площадь его горизонтального сечения.

4. Из условия задачи: \( V = {V_1} + {V_2} = {V_1}' + {V_2}' \)

\( \frac{{{V_1}}}{{{V_2}}} = 2;\frac{{{V_1}'}}{{{V_2}'}} = 3 \Rightarrow {V_2} = \frac{V}{3} \), \( {V_1} = \frac{{2V}}{3},{V_2}' = \frac{V}{4},{V_1}' = \frac{{3V}}{4} \)

где V — объём всего сосуда.

5. После объединения записанных выше выражений получим уравнение:

\( \frac{{3\nu RT}}{V} - \frac{{3\nu RT}}{{2V}} = \)\( \frac{{4(\nu - \Delta \nu )RT}}{V} - \frac{{4\nu RT}}{{3V}} \)

откуда получим: \( \Delta \nu = \frac{{7\nu }}{{24}} = \frac{{7 \cdot 1}}{{24}} \) ≈ 0,29 моль

Ответ: \( \Delta \nu \) ≈ 0,29 моль

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21454.

1. Запишем уравнение Менделеева — Клапейрона для газа в верхней и нижней частях сосуда в начальном равновесном состоянии: \( {p_1}{V_1} = \nu RT \), \( {p_2}{V_2} = \nu RT \), где \( {p_1} \), \( {p_2} \) — давление воздуха в верхней и нижней частях сосуда, \( {V_1} \), \( {V_2} \) — объёмы верхней и нижней частей сосуда.

2. Запишем уравнение Менделеева Клапейрона для газа в верхней и нижней частях сосуда после откачки воздуха: \( {p_1}'{V_1}' = (\nu - \Delta \nu )RT \), \( {p_2}'{V_2}' = \nu RT \) где \( {p_1}' \), \( {p_2}' \) — давление воздуха в верхней и нижней частях сосуда, \( {V_1}' \), \( {V_2}' \) — объёмы верхней и нижней частей сосуда.

3. Условие механического равновесия поршня в начальном состоянии: \( {p_2} - {p_1} = \frac{{Mg}}{S} \), а после откачки воздуха: \( {p_2}' - {p_1}' = \frac{{Mg}}{S} \), где M — масса поршня, S — площадь его горизонтального сечения.

4. Из условия задачи: \( V = {V_1} + {V_2} = {V_1}' + {V_2}' \)

\( \frac{{{V_1}}}{{{V_2}}} = 2;\frac{{{V_1}'}}{{{V_2}'}} = \frac{2}{3} \Rightarrow {V_2} = \frac{V}{3} \), \( {V_1} = \frac{{2V}}{3},{V_1}' = \frac{{2V}}{5},{V_2}' = \frac{{3V}}{5} \)

где V — объём всего сосуда.

5. После объединения записанных выше выражений получим уравнение:

\( \frac{{3\nu RT}}{V} - \frac{{3\nu RT}}{{2V}} = \)\( \frac{{5\nu RT}}{{3V}} - \frac{{5(\nu - \Delta \nu )RT}}{{2V}} \)

откуда получим: \( \Delta \nu = \frac{{14}}{{15}}\nu = \frac{{14 \cdot 1}}{{15}} \) ≈ 0,93 моль

Ответ: \( \Delta \nu \) ≈ 0,93 моль

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21446.