Линия заданий 25, ЕГЭ по физике

1. При подключении положительного вывода батареи к точке \( A \) потенциал точки \( A \) оказывается выше, чем потенциал точки \( B \), \( {\varphi _A} > {\varphi _B} \), поэтому ток через диод, подключённый параллельно резистору \( {R_1} \), не течёт. Эквивалентная схема цепи в этом случае имеет вид, изображённый на рисунке а. Общее сопротивление соединённых резисторов в первом случае равно

\( {R_{01}} = \frac{{\left( {{R_1} + {R_2}} \right){R_2}}}{{{R_1} + 2{R_2}}} \)

а потребляемая мощность

\( {P_1} = \frac{{{\cal E ^2}({R_1} + 2{R_2})}}{{({R_1} + {R_2}){R_2}}} \)

2. При изменении полярности подключения батареи \( {\varphi _A} < {\varphi _B} \) открытый диод оказывается подключён к резистору \( {R_1} \) параллельно, шунтируя его. Эквивалентная схема цепи в этом случае изображена на рисунок б. Общее сопротивление соединённых резисторов во втором случае равно

\( {R_{02}} = \frac{{{R_2}}}{2} \)

а потребляемая мощность

\( {P_2} = \frac{{2{\cal E ^2}}}{{{R_2}}} \)

3. Из этих уравнений получим: \( {R_2} = \frac{{2{\cal E ^2}}}{{{P_2}}} = \frac{{2 \cdot {{12}^2}}}{{7,2}} \) = 40 Ом

\( {R_1} = \frac{{2{\cal E ^2}{R_2} - {P_1}R_2^2}}{{{P_1}{R_2} - {\cal E ^2}}} = \)\( \frac{{2 \cdot {{12}^2} \cdot 40 - 6 \cdot {{40}^2}}}{{6 \cdot 40 - {{12}^2}}} = 20 \) Ом

Ответ: R₁ = 20 Ом, R₂ = 40 Ом

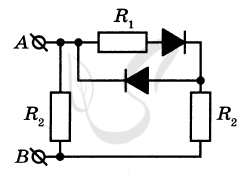
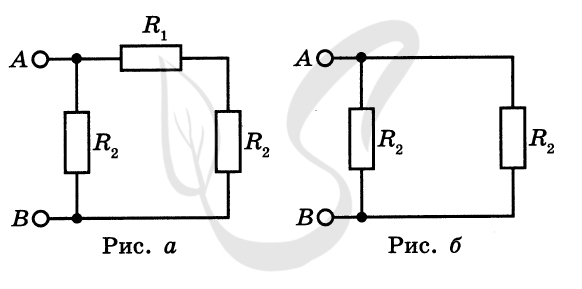
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21439.

1. При подключении положительного вывода батареи к точке \( A \) потенциал точки \( A \) оказывается выше, чем потенциал точки \( B \), \( {\varphi _A} > {\varphi _B} \), поэтому ток через диод, в подключённый параллельно резистору \( {R_1} \), не течёт. Эквивалентная схема цепи в этом случае имеет вид, изображённый на рисунке а. Суммарное сопротивление последовательно соединённых резисторов \( {R_0} = {R_1} + {R_2} \), а потребляемая мощность \( {P_1} = \frac{{{\cal E ^2}}}{{{R_1} + {R_2}}} \).

2. При изменении полярности подключения батареи \( {\varphi _A} < {\varphi _B} \), открытый диод оказывается подключён к резистору \( {R_1} \) параллельно, шунтируя его. Эквивалентная схема цепи в этом случае изображена на рисунок б. При этом потребляемая мощность увеличивается (так как знаменатель дроби уменьшается): \( {P_2} = \frac{{{\cal E ^2}}}{{{R_2}}} > {P_1} \)

3. Из этих уравнений: \( {R_1} = \frac{{{\cal E ^2}}}{{{P_1}}} - \frac{{{\cal E ^2}}}{{{P_2}}} \), \( {R_2} = \frac{{{\cal E ^2}}}{{{P_2}}} \)

4. Подставляя значения физических величин, указанные в условии, получаем: R₁ = 10 Ом, R₂ = 20 Ом

Ответ: R₁ = 10 Ом, R₂ = 20 Ом

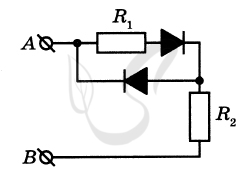
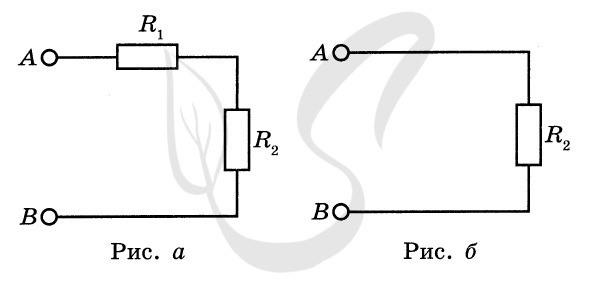
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21431.

1. На рисунке показаны силы, действующие на стержень с током:
— сила тяжести \( m\vec g \), направленная вертикально вниз
— сила реакции опоры \( {\vec N} \), направленная перпендикулярно к наклонной плоскости
— сила Ампера \( {{\vec F}_A} \), направленная горизонтально вправо, что вытекает из правила левой руки

2. Модуль силы Ампера \( {F_A} = IBL \), (1)
где \( L \) — длина стержня.

3. Систему отсчёта, связанную с наклонной плоскостью, считаем инерциальной. Запишем второй закон Ньютона в проекциях на ось x (см. рисунок):

\( m{a_x} = - mg\sin \alpha + IBL\cos \alpha \), (2)
где m — масса стержня.

Отсюда: \( {a_x} = IB(\frac{L}{m})\cos \alpha - g\sin \alpha \)\( = \frac{{4 \cdot 0,2}}{{0,1}} \cdot \cos 30^\circ - 10 \cdot \sin 30^\circ \approx \) = 1,9 м/с². (3)

Ответ: \( {a_x} \) = 1,9 м/с²

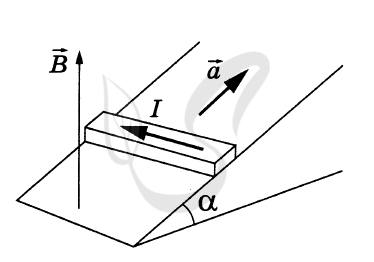
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21423.

1. На рисунке показаны силы, действующие на стержень с током:
— сила тяжести \( m\vec g \), направленная вертикально вниз
— сила реакции опоры \( {\vec N} \), направленная перпендикулярно к наклонной плоскости
— сила Ампера \( {{\vec F}_A} \), направленная горизонтально вправо, что вытекает из правила левой руки

2. Модуль силы Ампера \( {F_A} = IBL \), (1)
где \( L \) — длина стержня.

3. Систему отсчёта, связанную с наклонной плоскостью, считаем инерциальной. Запишем второй закон Ньютона в проекциях на ось x (см. рисунок):

\( m{a_x} = - mg\sin \alpha + IBL\cos \alpha \), (2)
где m — масса стержня.

Отсюда: \( I = \frac{m}{L} \cdot \frac{{{a_x} + g\sin \alpha }}{{B\cos \alpha }} = \)\( 0,1 \cdot \frac{{1,5 + 10 \cdot \sin 30^\circ }}{{0,3 \cdot \cos 30^\circ }} \) ≈ 2,5 А (3)

Ответ: \( I \) ≈ 2,5 А

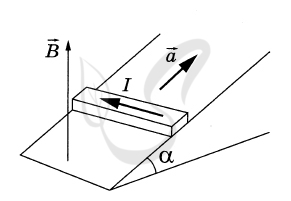
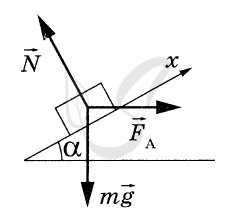
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21415.

1. При изменении магнитного потока через площадь рамки в ней возникнет ЭДС индукции

\( {\varepsilon _i} \) \( = - \frac{{\Delta \Phi }}{{\Delta t}} = - \frac{{\Delta {B_n}}}{{\Delta t}}S \)

2. Скорость изменения проекции вектора индукции магнитного поля \( {{B_n}} \) на перпендикуляр к плоскости рамки определим из графика: \( - \frac{{\Delta {B_n}}}{{\Delta t}} = \frac{{0,3}}{3} = 0,1 \) Тл/с.

3. Согласно закону Джоуля — Ленца в рамке выделится количество теплоты

\( Q = \frac{{\varepsilon _i^2}}{R}\tau = \frac{\tau }{R}{\left( {\frac{{\Delta {B_n}}}{{\Delta t}}S} \right)^2} \)

4. Так как площадь рамки \( S = {l^2} \), а её сопротивление \( R = \rho \frac{{4l}}{{{S_0}}} \), то получим:

\( {S_0} = \frac{{4\rho Q}}{{{l^3}\tau {{\left( {\Delta {B_n}/\Delta t} \right)}^2}}} = \)\( \frac{{4 \cdot 1,7 \cdot {{10}^{ - 8}} \cdot 53 \cdot {{10}^{ - 6}}}}{{{{10}^{ - 3}} \cdot 5 \cdot {{10}^{ - 2}}}} \) ≈ 0,072 · 10^-6 м² = 0,072 мм²

Ответ: S₀ = 0,072 мм²

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21407.

1. При изменении магнитного потока через площадь рамки в ней возникнет ЭДС индукции

\( {\varepsilon _i} \) \( = - \frac{{\Delta \Phi }}{{\Delta t}} = - \frac{{\Delta {B_n}}}{{\Delta t}}S \)

2. Скорость изменения проекции вектора индукции магнитного поля \( {{B_n}} \) на перпендикуляр к плоскости рамки определим из графика: \( - \frac{{\Delta {B_n}}}{{\Delta t}} = \frac{{0,3}}{3} = 0,1 \) Тл/с.

3. Согласно закону Джоуля — Ленца в рамке выделится количество теплоты

\( Q = \frac{{\varepsilon _i^2}}{R}\tau = \frac{\tau }{R}{\left( {\frac{{\Delta {B_n}}}{{\Delta t}}S} \right)^2} \)

4. Так как площадь рамки \( S = {l^2} \), а её сопротивление \( R = \rho \frac{{4l}}{{{S_0}}} \), то получим:

\( Q = \frac{{{S_0}{l^3}\tau {{\left( {\Delta {B_n}/\Delta t} \right)}^2}}}{{4\rho }} = \)\( \frac{{0,1 \cdot {{10}^{ - 6}} \cdot {{10}^{ - 3}} \cdot 4 \cdot {{10}^{ - 2}}}}{{4 \cdot 1,7 \cdot {{10}^{ - 8}}}} \) ≈ 59 · 10^-6 Дж = 59 мкДж

Ответ: Q₀ ≈ 59 мкДж

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21399.

1. При движении стержней с разными скоростями изменение потока вектора магнитной индукции, пронизывающего контур, за промежуток времени \( \Delta t \) определяется по формуле:

\( \Delta \Phi = Bl({\upsilon _1} - {\upsilon _2})\Delta t \)\( = Bl{\upsilon _{отн}}\Delta t \),

что приводит к возникновению в контуре ЭДС индукции.

Согласно закону Фарадея \( \cal E = - \) \( \frac{{\Delta \Phi }}{{\Delta t}} \) \( = - Bl{\upsilon _{отн}} \). Здесь мы пренебрегли самоиндукцией контура.


2. В соответствии с законом Ома для замкнутой цепи в контуре течёт ток:

\( I = \frac{{\left| \cal E \right|}}{{2R}} = \frac{{Bl{\upsilon _{отн}}}}{{2R}} \)


3. На проводники с током в магнитном поле действуют силы Ампера \( {{\vec F}_1} \) и \( {{\vec F}_2} \), \( {F_1} = {F_2} = IBl \), как показано на рисунке. Кроме этих сил на каждый стержень действует тормозящая сила трения \( {{\vec F}_{тр}} \).
Так как стержни движутся равномерно, сумма сил, приложенных к каждому стержню, равна нулю: \( F - {F_1} - {F_{тр}} = 0 \), \( {F_2} - {F_{тр}} = 0 \). Отсюда получим:

\( F = 2{F_1} = \frac{{{{(Bl)}^2}}}{R}{\upsilon _{отн}} \)

Следовательно,

\( R = \frac{{{{(Bl)}^2}{\upsilon _{отн}}}}{F} = \)\( \frac{{{{(2 \cdot 0,1)}^2} \cdot 0,75}}{{0,5}} = 0,06 \) Ом

Ответ: R = 0,06 Ом

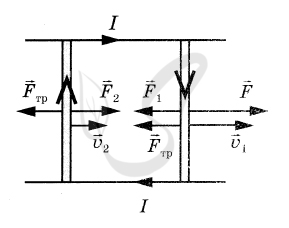
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21391.

1. При движении стержней с разными скоростями изменение потока вектора магнитной индукции, пронизывающего контур, за промежуток времени \( \Delta t \) определяется по формуле:

\( \Delta \Phi = Bl({\upsilon _1} - {\upsilon _2})\Delta t \)\( = Bl{\upsilon _{отн}}\Delta t \),

что приводит к возникновению в контуре ЭДС индукции.

Согласно закону Фарадея \( \cal E = - \) \( \frac{{\Delta \Phi }}{{\Delta t}} \) \( = - Bl{\upsilon _{отн}} \). Здесь мы пренебрегли самоиндукцией контура.


2. В соответствии с законом Ома для замкнутой цепи в контуре течёт ток:

\( I = \frac{{\left| \cal E \right|}}{{2R}} = \frac{{Bl{\upsilon _{отн}}}}{{2R}} \)


3. На проводники с током в магнитном поле действуют силы Ампера \( {{\vec F}_1} \) и \( {{\vec F}_2} \), \( {F_1} = {F_2} = IBl \), как показано на рисунке. Кроме этих сил на каждый стержень действует тормозящая сила трения \( {{\vec F}_{тр}} \).
Так как стержни движутся равномерно, сумма сил, приложенных к каждому стержню, равна нулю: \( F - {F_1} - {F_{тр}} = 0 \), \( {F_2} - {F_{тр}} = 0 \). Отсюда получим:

\( F = 2{F_1} = \frac{{{{(Bl)}^2}}}{R}{\upsilon _{отн}} \)

Следовательно,

\( {\upsilon _{отн}} = \frac{{FR}}{{{{(Bl)}^2}}} \) \( = \frac{{0,1 \cdot 0,1}}{{{{(1 \cdot 0,1)}^2}}} = 1 \) м/c

Ответ: \( {\upsilon _{отн}} \) = 1 м/c

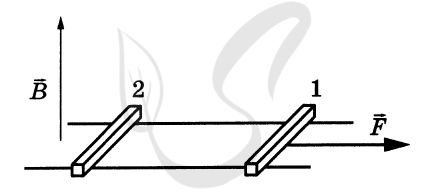
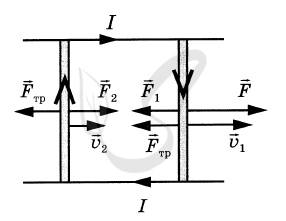
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21383.

При движении перемычки в однородном магнитном поле на её концах возникает ЭДС электромагнитной индукции: \({\cal E}\) = \( B\upsilon l \), где \( B \) — модуль индукции магнитного поля, \( \upsilon \) и \( l \) — соответственно скорость и длина перемычки. Согласно закону Ома для полной цепи в замкнутом контуре возникает индукционный ток:

\( {I_{инд}} = \frac{\cal E }{R} = \frac{{B\upsilon l}}{R} \),

где \( R \) — сопротивление перемычки. Поскольку скорость перемычки постоянна, то ЭДС и индукционный ток также будут постоянными. Согласно правилу Ленца индукционный ток, возникающий в контуре, будет направлен так, чтобы при движении перемычки своим магнитным полем препятствовать увеличению магнитного потока через площадку, охваченную контуром, т.е. индукционный ток будет направлен против часовой стрелки (см. рисунок). Благодаря появлению индукционного тока на перемычку со стороны магнитного поля начнёт действовать сила Ампера, направленная согласно правилу левой руки в противоположную движению сторону: \( {F_A} = B{I_{инд}}l = \frac{{{B^2}{l^2}\upsilon }}{R} \).

На перемычку действуют пять сил: сила тяжести \( m\vec g \), нормальная составляющая силы реакции опоры \( {\vec N} \), сила трения \( {{\vec F}_{тр}} \), сила Ампера \( {{\vec F}_A} \) и искомая сила \( {\vec F} \) (см. рисунок). Перемычка движется с постоянной скоростью, поэтому её ускорение равно нулю. Второй закон Ньютона в проекциях имеет вид: Ох: \( 0 = F - {F_{тр}} - {F_A} \); Оу: \( 0 = N - mg \). Сила трения скольжения \( {F_{тр}} = \mu N = \mu mg \). В итоге получаем:

\( F = \frac{{{{(Bl)}^2}\upsilon }}{R} - \mu mg = \frac{{{{(0,1 \cdot 1)}^2} \cdot 2}}{{0,025}} \)\( + 0,2 \cdot 0,37 \cdot 10 = 1,54 \) Н

Ответ: F = 1,54 Н

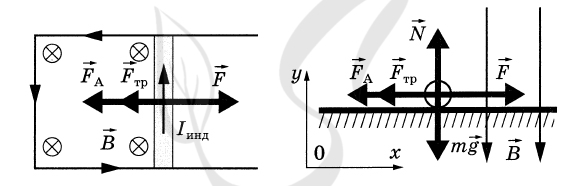
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21375.

При движении перемычки в однородном магнитном поле на её концах возникает ЭДС электромагнитной индукции: \({\cal E}\) = \( B\upsilon l \), где \( B \) — модуль индукции магнитного поля, \( \upsilon \) и \( l \) — соответственно скорость и длина перемычки. Согласно закону Ома для полной цепи в замкнутом контуре возникает индукционный ток:

\( {I_{инд}} = \frac{\cal E }{R} = \frac{{B\upsilon l}}{R} \),

где \( R \) — сопротивление перемычки. Поскольку скорость перемычки постоянна, то ЭДС и индукционный ток также будут постоянными. Согласно правилу Ленца индукционный ток, возникающий в контуре, будет направлен так, чтобы при движении перемычки своим магнитным полем препятствовать увеличению магнитного потока через площадку, охваченную контуром, т.е. индукционный ток будет направлен против часовой стрелки (см. рисунок). Благодаря появлению индукционного тока на перемычку со стороны магнитного поля начнёт действовать сила Ампера, направленная согласно правилу левой руки в противоположную движению сторону: \( {F_A} = B{I_{инд}}l = \frac{{{B^2}{l^2}\upsilon }}{R} \).

На перемычку действуют пять сил: сила тяжести \( m\vec g \), нормальная составляющая силы реакции опоры \( {\vec N} \), сила трения \( {{\vec F}_{тр}} \), сила Ампера \( {{\vec F}_A} \) и искомая сила \( {\vec F} \) (см. рисунок). Перемычка движется с постоянной скоростью, поэтому её ускорение равно нулю. Второй закон Ньютона в проекциях имеет вид: Ох: \( 0 = F - {F_{тр}} - {F_A} \); Оу: \( 0 = N - mg \). Сила трения скольжения \( {F_{тр}} = \mu N = \mu mg \). В итоге получаем:

\( R = \frac{{{{(Bl)}^2}\upsilon }}{{F - \mu mg}} = \)\( \frac{{{{(0,2 \cdot 1)}^2} \cdot 1,5}}{{1,6 - 0,2 \cdot 0,3 \cdot 10}} = 0,06 \) Ом

Ответ: R = 0,06 Ом

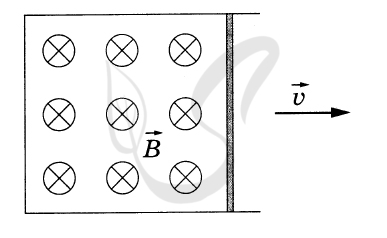
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21367.