Линия заданий 26, ЕГЭ по физике

Обоснование

Рассмотрим задачу в системе отсчёта, связанной с Землей. Будем считать эту систему отсчёта инерциальной (ИСО). Движение бруска поступательное, его можно описать моделью материальной точки.

Для нахождения скорости тел после абсолютно неупругого столкновения пластилинового тела с бруском используем закон сохранения импульса. Им можно воспользоваться, так как система является замкнутой, то есть внешние силы существенного действия на скорость, возникающую сразу после столкновения, не оказывают.

Для нахождения ускорения, с которым тела будут двигаться в дальнейшем, будем использовать второй закон Ньютона. Им можно воспользоваться, так как по условию задачи видно, что система является инерциальной.

Решение

Запишем закон сохранения импульса:

\( {m_{пл}} \cdot {\upsilon _{пл}} - {m_{бр}} \cdot {\upsilon _{бр}} = ({m_{пл}} + {m_{бр}}){\upsilon _0} \)

\( {\upsilon _0} = \frac{{m \cdot {\upsilon _{пл}} - 4m \cdot {\upsilon _{бр}}}}{{5m}} \) \( = \frac{{{\upsilon _{пл}} - 4{\upsilon _{бр}}}}{5} \),

\( {\upsilon _{нач}} = \frac{{150 - 4 \cdot 5}}{5} = -1 \) м/с

(знак «-» показывает направление скорости).
В дальнейшем тела будут двигаться равнозамедленно под действием постоянной силы трення. В этом случае можно воспользоваться вторым законом Ньютона:

\( 5 \cdot m \cdot a = \mu \cdot 5m \cdot g \Rightarrow \) \( a = \mu g = 1,7 \) м/с² - модуль ускорения.

Используем законы кинематики для движения тела с постоянным ускорением:

\( - 2aS = \upsilon _{кон}^2 - \upsilon _{нач}^2 \)

\( S = \frac{{\upsilon _{нач}^2 - \upsilon _{кон}^2}}{{2a}} \)

\( S = \frac{{{1^2} - {{0,7}^2}}}{{2 \cdot 1,7}} = 0,15 \) м

Ответ: S = 0,15 м

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21521.

Систему отсчёта, связанную с Землёй, можно считать инерциальной, а систему тел «пуля — ящик» замкнутой, т. к. возникающие ударные силы намного больше внешних сил, приложенных к телам системы. Так как пуля и ящик движутся поступательно, их можно считать материальными точками.

Воспользуемся законом сохранения импульса \( m\upsilon = Mu \)

откуда \( u = \frac{{m\upsilon }}{M} \)

Кинетическая энергия пули:

\( {E_{k1}} = \frac{{m{\upsilon ^2}}}{2} \)

ящика:

\( {E_{k2}} = \frac{{M{u^2}}}{2} = \frac{M}{2} \cdot \frac{{{m^2}{\upsilon ^2}}}{{{M^2}}} = \frac{{{m^2}{\upsilon ^2}}}{{2M}} \)

Доля переданной энергии:

\( \varepsilon = \frac{{{m^2}{\upsilon ^2}}}{{2M}} \cdot \frac{2}{{m{\upsilon ^2}}} = \frac{m}{M} \)

\( \varepsilon = \frac{{10 \cdot {{10}^{ - 3}}}}{4} \) = 0,0025

Ответ: 0,0025

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21520.

Потенциальная энергия взаимодействия тел при упругом ударе будет максимальна в момент наибольшей деформации тел, т.е. в тот момент, когда они перестанут сближаться и, следовательно, будут двигаться с одинаковой скоростью.

Таким образом, для интересующего нас момента времени закон сохранения импульса будет иметь вид

\( {m_1}{{\vec \upsilon }_1} + {m_2}{{\vec \upsilon }_2} = ({m_1} + {m_2})\vec u \)

Спроецируем это уравнение на направление движения первого тела:

\( {m_1}{\upsilon _1} - {m_2}{\upsilon _2} = ({m_1} + {m_2})u \)

По закону сохранения энергии

\( \frac{{{m_1}\upsilon _1^2}}{2} + \frac{{{m_2}\upsilon _2^2}}{2} \) = \( {E_T} + \frac{{({m_1} + {m_2}){u^2}}}{2} \)

Выразим неизвестную скорость \( u \) из закона сохранения импульса:

\( u = \frac{{{m_1}{\upsilon _1} - {m_2}{\upsilon _2}}}{{{m_1} + {m_2}}} \)

и подставим в закон сохранения энергии:

\( 2{E_T} = {m_1}\upsilon _1^2 + {m_2}\upsilon _2^2 - \) \( ({m_1} + {m_2})\frac{{{{({m_1}{\upsilon _1} - {m_2}{\upsilon _2})}^2}}}{{{{({m_1} + {m_2})}^2}}} \Rightarrow \)

\( 2{E_T}({m_1} + {m_2}) = m_1^2\upsilon _1^2 + {m_1}{m_2}\upsilon _1^2 \) \( + {m_2}{m_1}\upsilon _2^2 + m_2^2\upsilon _2^2 - m_1^2\upsilon _1^2 \) \( + 2{m_1}{m_2}{\upsilon _1}{\upsilon _2} - m_2^2\upsilon _2^2 \Rightarrow \)

\( 2{E_T}({m_1} + {m_2}) = {m_1}{m_2}(\upsilon _1^2 + 2{\upsilon _1}{\upsilon _2} + \upsilon _2^2) \Rightarrow \)

\( {E_T} = \frac{{{m_1}{m_2}{{({\upsilon _1} + {\upsilon _2})}^2}}}{{2({m_1} + {m_2})}} \) = 43 Дж

Ответ: \( {E_T} \) = 43 Дж

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21519.

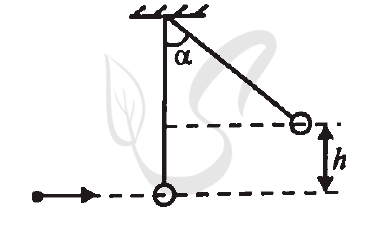
Обоснование

Рассмотрим задачу в системе отсчёта, связанной с Землёй. Будем считать эту систему отсчёта инерциальной (ИСО).

Шарик и пулю в данных условиях можно считать материальными точками. При отсутствии силы сопротивления воздуха и трения в инерциальной системе отсчёта для шарика и пули применим закон сохранения импульса при абсолютно неупругом ударе. Внешняя сила тяжести действует в течение очень малого промежутка времени взаимодействия, поэтому этим действием можно пренебречь.

После удара на шарик с пулей действует потенциальная сила (сила тяжести), сила натяжения нити перпендикулярна скорости шарика (а значит, работа этой силы равна нулю). Следовательно, механическая энергия сохраняется.

Решение

Во время взаимодействия пули с шариком механическая энергня не сохраняется, так как удар абсолютно неупругий, но сохраняется импульс, то есть

\( m{\upsilon _0} = (m + M)\upsilon \),

где \( \upsilon \) — скорость шарика вместе с пулей сразу же после удара.

По закону сохранения энергии

\( \frac{{(m + M){\upsilon ^2}}}{2} = \) \( (m + M)gh \Rightarrow {\upsilon ^2} = 2gh \)

Учитывая, что по закону сохранения импульса \( \upsilon = \frac{{m{\upsilon _0}}}{{m + M}} \) получим

\( \frac{{{m^2}\upsilon _0^2}}{{{{(m + M)}^2}}} = 2gh \)

Из рисунка ясно, что \( h = l - l\cos \alpha = l(1 - \cos \alpha ) \)

\( \frac{{{m^2}\upsilon _0^2}}{{{{(m + M)}^2}}} = 2gl(1 - \cos \alpha ) \)

\( 1 - \cos \alpha = \frac{{{m^2}\upsilon _0^2}}{{2gl{{(m + M)}^2}}} \)

\( \cos \alpha = 1 - \frac{{{m^2}\upsilon _0^2}}{{2gl{{(m + M)}^2}}} \)

\( \alpha = \arccos \left( {1 - \frac{{{m^2}\upsilon _0^2}}{{2gl{{(m + M)}^2}}}} \right) \) \( = \arccos (0,56) = 56^\circ \)

Ответ: \( \alpha \) = 56 °

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21518.

Обоснование
1. Рассмотрим задачу в системе отсчёта, связанной с Землёй. Будем считать эту систему отсчёта инерциальной (ИСО).
2. В ИСО изменение механической энергии тела равно работе всех приложенных к телу непотенциальных сил. При движении бруска вниз и вверх по наклонной плоскости на него действуют потенциальная сила тяжести и сила реакции опоры \( \vec N \), перпендикулярная перемещению бруска (трения нет, так как поверхность гладкая).
Поэтому работа силы \( \vec N \) при движении бруска по наклонной плоскости равна нулю.
Следовательно, механическая энергия бруска при его движении до удара сохраняется. Аналогично сохраняется механическая энергия бруска и при его движении после удара.
3. Закон сохранения импульса выполняется в ИСО в проекциях на выбранную ось, если сумма проекций внешних сил на эту ось равна нулю. В данном случае выбранную ось направим параллельно движению бруска. Проекции на эту наклонную ось сил тяжести, действующих на брусок и на пулю, не равны нулю.
Но надо учесть, что при столкновении бруска и пули импульс каждого из двух тел меняется на конечную величину, тогда как время столкновения мало. Следовательно, на каждое из двух тел в это время действовала огромная сила (это силы взаимодействия бруска и пули), по сравнению с которой сила тяжести ничтожна.
Поэтому при столкновении тел силы тяжести не учитываем. Вследствие этого при описании столкновения бруска с пулей соблюдается закон сохранения импульса для системы тел «брусок + пуля».

Решение
1. Найдём скорость \( {\upsilon _1} \), которую брусок приобрёл, пройдя путь х. Используем закон сохранения механической энергии:
\( Mgx\sin = \frac{{M\upsilon _1^2}}{2} \) , \( {\upsilon _1} = \sqrt {2gx\sin \alpha } \)
2. Учитывая абсолютно неупругий удар пули и бруска, запишем закон сохранения импульса для этих тел:
\( m\upsilon - M{\upsilon _1} = \left( {M + m} \right){\upsilon _2} \) ,
где \( \upsilon \) — скорость пули, \( {\upsilon _2} \) — скорость, которую приобретут тела после абсолютно неупругого удара.
3. По закону сохранения механической энергии бруска при его подъёме по наклонной плоскости на расстояние S:
\( \frac{{\left( {M + m} \right)\upsilon _2^2}}{2} = \left( {M + m} \right)gS\sin \alpha \) , \( {\upsilon _2} = \sqrt {2gS\sin \alpha } \)
4. Тогда
\( \upsilon = \frac{M}{m}\sqrt {2gx\sin \alpha } + \left( {\frac{M}{m} + 1} \right) \)\( \sqrt {2gS\sin \alpha } \)
\( \upsilon = 50\sqrt {2 \cdot 10 \cdot 3,6 \cdot 0,5} + 51 \)\( \cdot \sqrt {2 \cdot 10 \cdot 2,5 \cdot 0,5} = 555 \) м/с
Ответ: \( \upsilon = 555 \) м/с

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21091.

Обоснование
1. Рассмотрим задачу в системе отсчёта, связанной с Землёй. Будем считать эту систему отсчёта инерциальной (ИСО).
2. В ИСО изменение механической энергии тела равно работе всех приложенных к телу непотенциальных сил. При движении бруска вниз и вверх по наклонной плоскости на него действуют потенциальная сила тяжести и сила реакции опоры \( \vec N \), перпендикулярная перемещению бруска (трения нет, так как поверхность гладкая).
Поэтому работа силы \( \vec N \) при движении бруска по наклонной плоскости равна нулю.
Следовательно, механическая энергия бруска при его движении до удара сохраняется. Аналогично сохраняется механическая энергия бруска и при его движении после удара.
3. Закон сохранения импульса выполняется в ИСО в проекциях на выбранную ось, если сумма проекций внешних сил на эту ось равна нулю. В данном случае выбранную ось направим параллельно движению бруска. Проекции на эту наклонную ось сил тяжести, действующих на брусок и на пулю, не равны нулю.
Но надо учесть, что при столкновении бруска и пули импульс каждого из двух тел меняется на конечную величину, тогда как время столкновения мало. Следовательно, на каждое из двух тел в это время действовала огромная сила (это силы взаимодействия бруска и пули), по сравнению с которой сила тяжести ничтожна.
Поэтому при столкновении тел силы тяжести не учитываем. Вследствие этого при описании столкновения бруска с пулей соблюдается закон сохранения импульса для системы тел «брусок + пуля».

Решение
1. Найдём скорость \( {\upsilon _1} \), которую брусок приобрёл, пройдя путь х. Используем закон сохранения механической энергии:
\( Mgx\sin = \frac{{M\upsilon _1^2}}{2} \) , \( {\upsilon _1} = \sqrt {2gx\sin \alpha } \)
2. Учитывая абсолютно неупругий удар пули и бруска, запишем закон сохранения импульса для этих тел:
\( m\upsilon - M{\upsilon _1} = \left( {M + m} \right){\upsilon _2} \) ,
где \( \upsilon \) — скорость пули, \( {\upsilon _2} \) — скорость, которую приобретут тела после абсолютно неупругого удара.
3. По закону сохранения механической энергии бруска при его подъёме по наклонной плоскости на расстояние S:
\( \frac{{\left( {M + m} \right)\upsilon _2^2}}{2} = \left( {M + m} \right)gS\sin \alpha \) , \( {\upsilon _2} = \sqrt {2gS\sin \alpha } \)
4. Тогда
\( m = \frac{{M\sqrt {2g\sin \alpha } \left( {\sqrt x + \sqrt S } \right)}}{{\upsilon - \sqrt {2gS\sin a} }} = \) \( \frac{{0,25\sqrt {2 \cdot 10 \cdot \sin 30^\circ } \left( {\sqrt {3,6} + \sqrt {2,5} } \right)}}{{555 - \sqrt {2 \cdot 10 \cdot 2,5 \cdot \sin 30^\circ } }} \) \( = 0,005 \) кг
Ответ: m = 5 г

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21090.

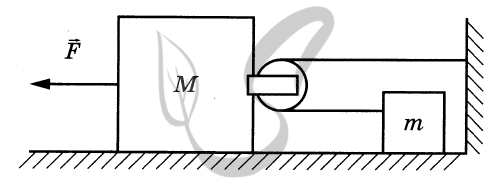
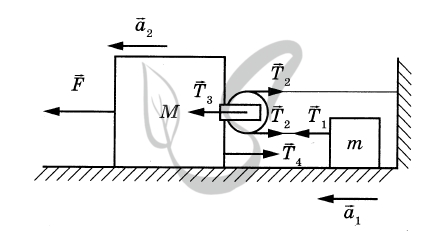
Обоснование
1. Рассмотрим задачу в системе отсчёта, связанной с Землёй. Будем считать эту систему отсчёта инерциальной (ИСО).
2. Брусок и тело движутся поступательно, поэтому описываем их моделью материальной точки независимо от их размеров.
3. Из пп. 1 и 2 следует, что движение бруска и тела в ИСО описывается вторым законом Ньютона.
4. Нить невесома, блок идеален (масса блока ничтожна, трения нет), поэтому модуль силы натяжения нити в любой её точке один и тот же.
5. Нить нерастяжима, поэтому модули ускорений подвижного блока и тела т при их прямолинейном поступательном движении отличаются в 2 раза.

Решение

Систему отсчёта, связанную с Землёй, будем считать инерциальной. Запишем второй закон Ньютона в проекциях на горизонтальную ось для тела и бруска:
\( m{a_1} = {T_1} \) ; \( M{a_2} = F - {T_4} \) , где \( {a_1} \) и \( {a_2} \) — ускорения тела и бруска, \( {T_1} \) — сила натяжения нити, \( {T_2} \) — сила, с которой блок действует на брусок.
Запишем второй закон Ньютона для невесомого блока: \( 0 = {T_3} - 2{T_2} \), где \( {T_3} \) — сила, с которой брусок действует на блок, \( {T_2} \) — сила натяжения нити, действующая на блок.
Поскольку нить невесома, то \( \left| {{{\vec T}_1}} \right| = \left| {{{\vec T}_2}} \right| = T \). По третьему закону Ньютона \( {{\vec T}_3} = - {{\vec T}_4} \), или \( \left| {{{\vec T}_3}} \right| = \left| {{{\vec T}_4}} \right| \).
Ускорение бруска массой M в 2 раза меньше ускорения тела массой т, так как за одно и то же время перемещение тела в 2 раза больше перемещения бруска: \( \left| {{{\vec T}_3}} \right| = \left| {{{\vec T}_4}} \right| \).
Приходим к системе уравнений:
\( \left\{ \begin{array}{l}
F - 2T = M{a_2}\\
T = m \cdot 2{a_2}
\end{array} \right. \)
, откуда \( {a_2} = \frac{F}{{M + 4m}} \)
\( {a_2} = \frac{F}{{M + 4m}} = \) \( \frac{{10}}{{2 + 4 \cdot 0,75}} = 2 \) м/с²
Ответ: 2 м/с²

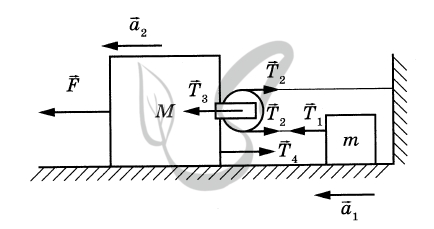
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21089.

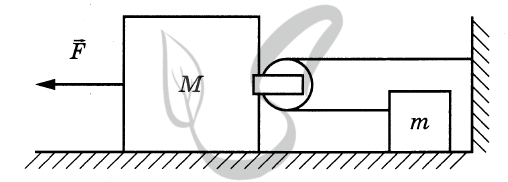
Обоснование
1. Рассмотрим задачу в системе отсчёта, связанной с Землёй. Будем считать эту систему отсчёта инерциальной (ИСО).
2. Брусок и тело движутся поступательно, поэтому описываем их моделью материальной точки независимо от их размеров.
3. Из пп. 1 и 2 следует, что движение бруска и тела в ИСО описывается вторым законом Ньютона.
4. Нить невесома, блок идеален (масса блока ничтожна, трения нет), поэтому модуль силы натяжения нити в любой её точке один и тот же.
5. Нить нерастяжима, поэтому модули ускорений подвижного блока и тела т при их прямолинейном поступательном движении отличаются в 2 раза.

Решение

Систему отсчёта, связанную с Землёй, будем считать инерциальной. Запишем второй закон Ньютона в проекциях на горизонтальную ось для тела и бруска:
\( m{a_1} = {T_1} \) ; \( M{a_2} = F - {T_4} \) , где \( {a_1} \) и \( {a_2} \) — ускорения тела и бруска, \( {T_1} \) — сила натяжения нити, \( {T_2} \) — сила, с которой блок действует на брусок.
Запишем второй закон Ньютона для невесомого блока: \( 0 = {T_3} - 2{T_2} \), где \( {T_3} \) — сила, с которой брусок действует на блок, \( {T_2} \) — сила натяжения нити, действующая на блок.
Поскольку нить невесома, то \( \left| {{{\vec T}_1}} \right| = \left| {{{\vec T}_2}} \right| = T \). По третьему закону Ньютона \( {{\vec T}_3} = - {{\vec T}_4} \), или \( \left| {{{\vec T}_3}} \right| = \left| {{{\vec T}_4}} \right| \).
Ускорение бруска массой M в 2 раза меньше ускорения тела массой т, так как за одно и то же время перемещение тела в 2 раза больше перемещения бруска: \( \left| {{{\vec T}_3}} \right| = \left| {{{\vec T}_4}} \right| \).
Приходим к системе уравнений:
\( \left\{ \begin{array}{l}
F - 2T = M{a_2}\\
T = m \cdot 2{a_2}
\end{array} \right. \)
, откуда \( {a_2} = \frac{F}{{M + 4m}} \)
\( {a_1} = 2{a_2} = \frac{{2F}}{{M + 4m}} = \) \( \frac{{2 \cdot 10}}{{2 + 4 \cdot 0,75}} = 4 \) м/с²
Ответ: 4 м/с²

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21088.

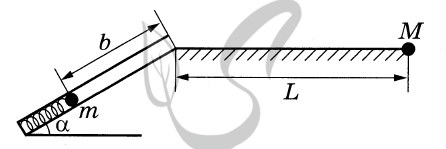
Обоснование
1. Рассмотрим задачу в системе отсчёта, связанной с Землёй. Будем считать эту систему отсчёта инерциальной (ИСО).
2. Шарик имеет малые размеры по сравнению с размерами пружины и дальностью полёта, поэтому описываем его моделью материальной точки.
3. В процессе движения шарика по стволу к верхней точке своей траектории на него действуют сила тяжести \( m\vec g \), сила упругости \( {{\vec F}_y} \) и сила реакции опоры \( {\vec N} \).
Изменение механической энергии шарика в ИСО равно работе всех непотенциальных сил, приложенных к телу. В данном случае единственной такой силой является сила реакции опоры \( {\vec N} \). В каждой точке траектории \( \vec N \bot \vec \upsilon \), где \( {\vec \upsilon } \) - скорость шарика, поэтому работа силы \( {\vec N} \) равна нулю, следовательно, механическая энергия шарика при его движении по стволу сохраняется.

Решение
По закону сохранения механической энергии
\( {E_0} = \frac{{m\upsilon _0^2}}{2} + mgb\sin \alpha \) ,
где \( {E_0} \) — энергия сжатой пружины, а \( {\upsilon _0} \) — скорость шарика в момент вылета из дула ружья.
Согласно формулам кинематики тела, брошенного под углом к горизонту,
\( L = {\upsilon _0}t\cos \alpha ,t = \frac{{2{\upsilon _0}\sin \alpha }}{g} \) , где t — время полета. Следовательно, расстояние
\( L = \frac{{\upsilon _0^2}}{g}\sin 2\alpha \)
Комбинируя формулы (1) и (2), находим:
\( m = \frac{{{E_0}}}{{g\left( {\frac{L}{{2\sin 2\alpha }} + b\sin \alpha } \right)}} = \) \( \frac{{0,25}}{{10 \cdot \left( {\frac{1}{{2 \cdot 0,866}} + 0,5 \cdot 0,5} \right)}} \) \( \approx 0,03 \) кг = 30 г
Ответ: 30 г

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21087.

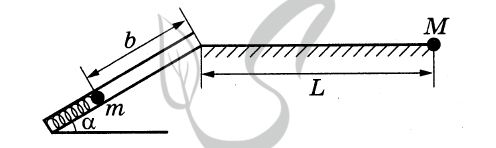
Обоснование
1. Рассмотрим задачу в системе отсчёта, связанной с Землёй. Будем считать эту систему отсчёта инерциальной (ИСО).
2. Шарик имеет малые размеры по сравнению с размерами пружины и дальностью полёта, поэтому описываем его моделью материальной точки.
3. В процессе движения шарика по стволу к верхней точке своей траектории на него действуют сила тяжести \( m\vec g \), сила упругости \( {{\vec F}_y} \) и сила реакции опоры \( {\vec N} \).
Изменение механической энергии шарика в ИСО равно работе всех непотенциальных сил, приложенных к телу. В данном случае единственной такой силой является сила реакции опоры \( {\vec N} \). В каждой точке траектории \( \vec N \bot \vec \upsilon \), где \( {\vec \upsilon } \) - скорость шарика, поэтому работа силы \( {\vec N} \) равна нулю, следовательно, механическая энергия шарика при его движении по стволу сохраняется.

Решение
По закону сохранения механической энергии
\( {E_0} = \frac{{m\upsilon _0^2}}{2} + mgb\sin \alpha \) ,
где \( {E_0} \) — энергия сжатой пружины, а \( {\upsilon _0} \) — скорость шарика в момент вылета из дула ружья.
Согласно формулам кинематики тела, брошенного под углом к горизонту,
\( L = {\upsilon _0}t\cos \alpha ,t = \frac{{2{\upsilon _0}\sin \alpha }}{g} \) , где t — время полета. Следовательно, расстояние
\( L = \frac{{\upsilon _0^2}}{g}\sin 2\alpha \)
Комбинируя формулы (1) и (2), находим:
\( L = \frac{2}{{mg}}\sin 2\alpha \left( {{E_0} - mgb\sin \alpha } \right) \) \( = \frac{2}{{5 \cdot {{10}^{ - 2}} \cdot 10}}\sin 60^\circ \left( {0,41 - 5 \cdot {{10}^{ - 2}} \cdot 10 \cdot 0,5 \cdot \sin 30^\circ } \right) \) \( \approx 1 \) м
Ответ: 1 м

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21086.