


После прохождения светом дифракционной решётки на экране будет формироваться
дифракционный спектр, представляющий собой симметричные относительно центра
повторяющиеся светлые полосы. Под углом \( \alpha \) к нормали будет наблюдаться \( k \)-й
максимум, если \( d\sin \alpha = k\lambda \), где \( \lambda = \frac{c}{\nu } \). Максимальный порядок
наблюдаться под углом \( \alpha \) = 90°.
Следовательно, для максимального порядка спектра получим:
\( k = \frac{{d\nu }}{c} = \frac{{{{10}^{ - 3}} \cdot 5 \cdot {{10}^{14}}}}{{500 \cdot 3 \cdot {{10}^8}}} \) ≈ 3,3
Максимальный порядок спектра k = 3
Ответ: k = 3
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21437.
После прохождения светом дифракционной решётки на экране будет формироваться
дифракционный спектр, представляющий собой симметричные относительно центра
повторяющиеся светлые полосы. Под углом \( \alpha \) к нормали будет наблюдаться \( k \)-й
максимум, если \( d\sin \alpha = k\lambda \), где \( \lambda = \frac{c}{\nu } \). Максимальный порядок спектра будет
наблюдаться под углом \( \alpha \) = 90°.
Следовательно, для максимального порядка спектра получим:
\( k = \frac{{d\nu }}{c} = \frac{{{{10}^{ - 3}} \cdot 5,6 \cdot {{10}^{14}}}}{{300 \cdot 3 \cdot {{10}^8}}} \) ≈ 6,2
Максимальный порядок спектра k = 6
Ответ: k = 6
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21429.
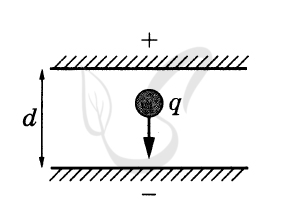
На каплю действуют сила тяжести, направленная вниз, и сила со стороны
электростатического поля, направленная вверх, так как капля заряжена
отрицательно. Для того чтобы капля двигалась с постоянной скоростью, эти силы
должны быть равны но модулю: \( mg = \left| q \right|E \).
Напряжённость однородного электростатического поля конденсатора связана
с напряжением между пластинами соотношением \( E = \frac{U}{d} \).
Следовательно, масса капли
\( m = \frac{{\left| q \right|U}}{{dg}} = \)\( \frac{{8 \cdot {{10}^{ - 11}} \cdot {{10}^4}}}{{2 \cdot {{10}^{ - 2}} \cdot 10}} = 4 \cdot {10^{ - 6}} \) кг = 4 мг
Ответ: m = 4 мг
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21421.
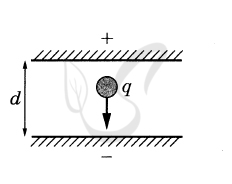
Скорость капли постоянна, если равнодействующая сил, действующих на каплю,
равна нулю. На каплю действуют сила тяжести, направленная вниз, и сила
со стороны электростатического поля, которая для постоянства скорости должна
быть направлена вверх. Следовательно, капля заряжена отрицательно. Для того
чтобы капля двигалась с постоянной скоростью, эти силы должны быть равны
по модулю: \( mg = \left| q \right|E \).
Напряжённость однородного электростатического поля конденсатора связана
с напряжением между пластинами соотношением \( E = \frac{U}{d} \).
Следовательно, заряд капли
\( q = - \frac{{mdg}}{U} = \)\( \frac{{5 \cdot {{10}^{ - 6}} \cdot 2 \cdot {{10}^{ - 2}} \cdot 10}}{{{{10}^4}}} = - {10^{ - 10}} \) Кл
Ответ: q = -10-10 Кл
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21413.
1. Так как после достижения теплового равновесия температура воды выше нуля,
то это означает, что весь первоначальный кусок льда растаял.
2. Так как потери по условию отсутствуют, а лёд первоначально находится при
температуре плавления, то всё количество теплоты, полученное льдом при
охлаждении воды от 45 до 5 °С, пошло на плавление льда и нагревание талой
воды от 0 до 5 °С. Запишем уравнение теплового баланса:
\( \left| {{Q_{отд}}} \right| = \left| {{Q_{пол}}} \right| \) или \( c{m_{вод}}({t_{гор}} - {t_{хол}}) = \lambda {m_{лед}} + c{m_{лед}}({t_{хол}} - {t_{плав}}) \), откуда
\( {m_{лед}} = \frac{{c{m_{вод}}({t_{гор}} - {t_{хол}})}}{{\lambda + c({t_{хол}} - {t_{плав}})}} \) (2)
где \( c \) и \( {{m_{вод}}} \) — удельная теплоёмкость и масса воды соответственно, \( \lambda \) и \( {{m_{лед}}} \) — удельная теплота плавления и масса растаявшего льда, \( {{t_{гор}}} \) и \( {{t_{хол}}} \) — начальная и конечная температура воды, \( {{t_{плав}}} \) — температура плавления льда.
3. Подставив числовые значения в (2), получим искомую величину:
\( {m_{лед}} = \frac{{4200 \cdot 0,45 \cdot (45 - 5)}}{{3,3 \cdot {{10}^5} + 4200(5 - 0)}} \) ≈ 0,215 кг ≈ 215 г
Ответ: mлед = 215 г
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21405.
1. Так как после достижения теплового равновесия температура воды выше нуля,
то это означает, что весь первоначальный кусок льда растаял.
2. Так как потери по условию отсутствуют, а лёд первоначально находится при
температуре плавления, то всё количество теплоты, полученное льдом при
охлаждении воды от 55 до 5 °С, пошло на плавление льда и нагревание талой
воды от 0 до 5 °С. Запишем уравнение теплового баланса:
\( \left| {{Q_{отд}}} \right| = \left| {{Q_{пол}}} \right| \) или \( c{m_{вод}}({t_{гор}} - {t_{хол}}) = \lambda {m_{лед}} + c{m_{лед}}({t_{хол}} - {t_{плав}}) \), откуда
\( {m_{вод}} = \frac{{{m_{лед}}(\lambda + ({t_{хол}} - {t_{плав}}))}}{{c({t_{гор}} - {t_{хол}})}} \) (2)
где \( c \) и \( {{m_{вод}}} \) — удельная теплоёмкость и масса воды соответственно, \( \lambda \) и \( {{m_{лед}}} \) — удельная теплота плавления и масса растаявшего льда, \( {{t_{гор}}} \) и \( {{t_{хол}}} \) — начальная и конечная температура воды, \( {{t_{плав}}} \) — температура плавления льда.
3. Подставив числовые значения в (2), получим искомую величину:
\( {m_{вод}} = \frac{{0,3 \cdot (3,3 \cdot {{10}^5} + 4200 \cdot (5 - 0))}}{{4200 \cdot (55 - 5)}} \) ≈ 0,5 кг
Ответ: mвод = 0,5 кг
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21397.

Максимальная энергия магнитного поля катушки равна \( {W_M} = \frac{{LI_M^2}}{2} \)
‚ где L — индуктивность катушки колебательного контура, \( {I_M} \) — амплитуда силы тока
в катушке.
Согласно формуле Томсона период электромагнитных колебаний в контуре
определяется соотношением \( T = 2\pi \sqrt {LC} \), где \( C \) — электроёмкость конденсатора
колебательного контура.
Согласно данным, приведённым в таблице, \( {I_M} = 4 \cdot {10^{ - 3}}A \) и \( T = 8 \cdot {10^{ - 6}} \) с.
В итоге получим:
\( {W_M} = \frac{{{T^2}I_M^2}}{{8{\pi ^2}C}} = \)\( \frac{{64 \cdot {{10}^{ - 12}} \cdot 16 \cdot {{10}^{ - 6}}}}{{8 \cdot {{3,14}^2} \cdot 405 \cdot {{10}^{ - 12}}}} \) ≈ 32 · 10-9 Дж ≈ 32 нДж
Ответ: \( {W_M} \) ≈ 32 нДж
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21389.

Максимальная энергия электрического поля конденсатора равна \( {W_M} = \frac{{CU_M^2}}{2} \)‚
где
\( C \) — электроёмкость конденсатора колебательного контура, \( {U_M} \) — амплитуда
напряжения на конденсаторе.
Согласно формуле Томсона период электромагнитных колебаний в контуре
определяется соотношением \( T = 2\pi \sqrt {LC} \), где \( L \) — индуктивность катушки
колебательного контура.
Согласно данным, приведённым в таблице, \( {U_M} \) = 40 В и \( T \) = 8 · 10-6 с.
В итоге получим: \( {W_M} = \frac{{{T^2}U_M^2}}{{8{\pi ^2}L}} = \)\( \frac{{64 \cdot {{10}^{ - 12}} \cdot {{40}^2}}}{{8 \cdot {{3,14}^2} \cdot 4,3 \cdot {{10}^{ - 3}}}} \)\( \approx 300 \cdot {10^{ - 9}} \) Дж = 0,3 мкДж
Ответ: \( {W_M} \) ≈ 0,3 мкДж
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21381.
1. Так как потери по условию отсутствуют, то всё количество теплоты, отданное
водой при охлаждении от начальной температуры \( {t_1} \) до \( {t_2} \) = 0 °С, пошло на плавление
льда, имеющего температуру плавления. Запишем уравнение теплового баланса:
\( \left| {{Q_{отд}}} \right| = \left| {{Q_{пол}}} \right| \) или \( c{m_{вод}}({t_1} - {t_2}) = \lambda {m_{лед}} \),
откуда \( {t_1} = \frac{{\lambda {m_{лед}}}}{{c{m_{вод}}}} + {t_2} \),
где \( c \) и \( {{m_{вод}}} \) - удельная теплоёмкость и масса воды соответственно, \( \lambda \) и \( {{m_{лед}}} \) - удельная теплота плавления и масса растаявшего льда.
2. Подставив числовые значения, получим искомую величину:
\( {t_1} = \frac{{3,3 \cdot {{10}^5} \cdot 0,14}}{{4200 \cdot 0,25}} + 0 \) = 44 °С
Ответ: \( {t_1} \) = 44 °С
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21373.
1. Так как потери энергии по условию отсутствуют, то всё количество теплоты,
отданное водой при охлаждении от начальной температуры \( {t_1} \) до \( {t_2} \) =0 °С, пошло
на плавление льда, имеющего температуру плавления. Запишем уравнение
теплового баланса:
\( \left| {{Q_{отд}}} \right| = \left| {{Q_{пол}}} \right| \)
\( c{m_{вод}}({t_1} - {t_2}) = \lambda {m_{лед}} \),
откуда \( {m_{лед}} = \frac{{c{m_{вод}}({t_1} - {t_2})}}{\lambda } \),
где \( c \) и \( {{m_{вод}}} \) - удельная теплоёмкость и масса воды соответственно, \( \lambda \) и \( {m_{лед}} \) — удельная теплота плавления и масса растаявшего льда.
2. Подставив числовые значения, получим искомую величину:
\( {m_{лед}} = \frac{{4200 \cdot 0,4(55 - 0)}}{{3,3 \cdot {{10}^5}}} \) = 0,28 кг
Ответ: \( {m_{лед}} \) = 0,28 кг
P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21365.