Линия заданий 26, ЕГЭ по физике

Обоснование
1. Рассмотрим задачу в системе отсчёта, связанной с Землёй. Будем считать эту систему отсчёта инерциальной (ИСО).
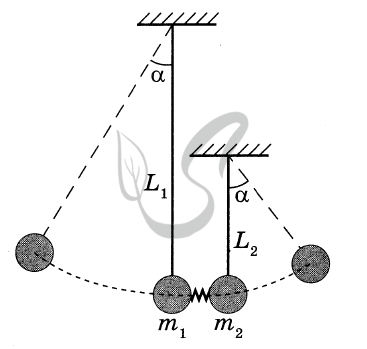
2. Шарики имеют малые размеры по сравнению с длиной нити, поэтому описываем их моделью материальной точки.
3. При пережигании нити пружина толкает оба шарика, действуя на шарики внутренней силой - силой упругости, все внешние силы, действующие на систему двух шариков, направлены вертикально (силы тяжести и натяжения нитей), поэтому сохраняется горизонтальная проекция импульса системы шариков, поскольку импульс пружины пренебрежимо мал из-за её малой массы.
4. В процессе движения каждого шарика на нити к верхней точке своей траектории на каждый из них действуют сила тяжести \( m\vec g \) и сила натяжения нити \( (\vec T) \).
Изменение механической энергии шарика в ИСО равно работе всех непотенциальных сил, приложенных к нему. В данном случае единственной такой силой является сила натяжения нити \( (\vec T) \). В каждой точке траектории \( \vec T \bot \vec \upsilon \), где \( (\vec \upsilon ) \) - скорость шарика, поэтому работа силы \( (\vec T) \) равна нулю, а механическая энергия каждого шарика на этом участке его движения сохраняется.

Решение
После пережигания нити пружина распрямится, сообщая шарикам начальные скорости \( {{\vec \upsilon }_1} \) и \( {{\vec \upsilon }_2} \). Запишем закон сохранения импульса для системы шариков в проекциях на ось x (см. рисунок):
\( 0 = - {m_1}{\upsilon _1} + {m_2}{\upsilon _2} \)
Для описания дальнейшего движения каждого шарика воспользуемся законом сохранения полной механической энергии:
\( \frac{{{m_1}\upsilon _1^2}}{2} = {m_1}g{h_1} = {m_1}g{L_1}\left( {1 - \cos \alpha } \right) \)
\( \frac{{{m_2}\upsilon _2^2}}{2} = {m_2}g{h_2} = {m_2}g{L_2}\left( {1 - \cos \alpha } \right) \)
Поделив эти равенства друг на друга почленно, получим:
\( \frac{{{L_1}}}{{{L_2}}} = {\left( {\frac{{{\upsilon _1}}}{{{\upsilon _2}}}} \right)^2} \)
Из закона сохранения импульса следует, что \( \frac{{{\upsilon _1}}}{{{\upsilon _2}}} = \frac{{{m_1}}}{{{m_2}}} \)
Поэтому \( \frac{{{m_2}}}{{{m_1}}} = \sqrt {\frac{{{L_1}}}{{{L_2}}}} = \sqrt 2 \approx 1,4 \)
Ответ: \( \frac{{{m_2}}}{{{m_1}}} \approx 1,4 \)

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21085.

Обоснование
1. Рассмотрим задачу в системе отсчёта, связанной с Землёй. Будем считать эту систему отсчёта инерциальной (ИСО).
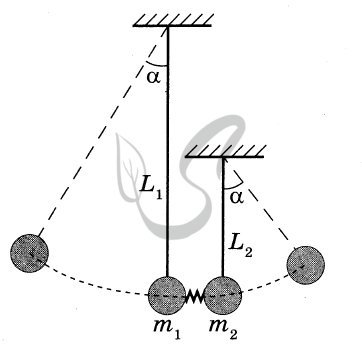
2. Шарики имеют малые размеры по сравнению с длиной нити, поэтому описываем их моделью материальной точки.
3. При пережигании нити пружина толкает оба шарика, действуя на шарики внутренней силой - силой упругости, все внешние силы, действующие на систему двух шариков, направлены вертикально (силы тяжести и натяжения нитей), поэтому сохраняется горизонтальная проекция импульса системы шариков, поскольку импульс пружины пренебрежимо мал из-за её малой массы.
4. В процессе движения каждого шарика на нити к верхней точке своей траектории на каждый из них действуют сила тяжести \( m\vec g \) и сила натяжения нити \( (\vec T) \).
Изменение механической энергии шарика в ИСО равно работе всех непотенциальных сил, приложенных к нему. В данном случае единственной такой силой является сила натяжения нити \( (\vec T) \). В каждой точке траектории \( \vec T \bot \vec \upsilon \), где \( (\vec \upsilon ) \) - скорость шарика, поэтому работа силы \( (\vec T) \) равна нулю, а механическая энергия каждого шарика на этом участке его движения сохраняется.

Решение
После пережигания нити пружина распрямится, сообщая шарикам начальные скорости \( {{\vec \upsilon }_1} \) и \( {{\vec \upsilon }_2} \). Запишем закон сохранения импульса для системы шариков в проекциях на ось x (см. рисунок):
\( 0 = - {m_1}{\upsilon _1} + {m_2}{\upsilon _2} \)
Для описания дальнейшего движения каждого шарика воспользуемся законом сохранения полной механической энергии:
\( \frac{{{m_1}\upsilon _1^2}}{2} = {m_1}g{h_1} = {m_1}g{L_1}\left( {1 - \cos \alpha } \right) \)
\( \frac{{{m_2}\upsilon _2^2}}{2} = {m_2}g{h_2} = {m_2}g{L_2}\left( {1 - \cos \alpha } \right) \)
Поделив эти равенства друг на друга почленно, получим:
\( \frac{{{L_1}}}{{{L_2}}} = {\left( {\frac{{{\upsilon _1}}}{{{\upsilon _2}}}} \right)^2} \)
Из закона сохранения импульса следует, что \( \frac{{{\upsilon _1}}}{{{\upsilon _2}}} = \frac{{{m_2}}}{{{m_1}}} \)
Поэтому \( \frac{{{L_1}}}{{{L_2}}} = {\left( {\frac{{{m_2}}}{{{m_1}}}} \right)^2} = {1,5^2} = 2,25 \)
Ответ: \( \frac{{{L_1}}}{{{L_2}}} = 2,25 \)

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21084.

Обоснование
Задачу будем решать в инерциальной системе отсчёта, связанной с поверхностью стола. Будем применять для грузов и бруска законы Ньютона, справедливые для материальных точек, поскольку тела движутся поступательно. Трением в оси блока и трением о воздух, а также массой блока пренебрежём.
Так как нить нерастяжима и длина пружины постоянна, ускорения обоих брусков и груза равны по модулю:
\( \left| {{{\vec a}_1}} \right| = \left| {{{\vec a}_2}} \right| = \left| {{{\vec a}_3}} \right| = a \)
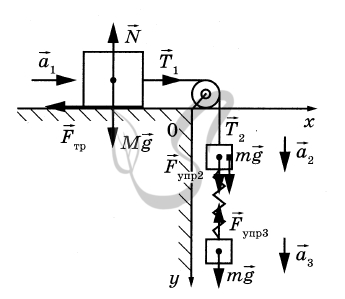
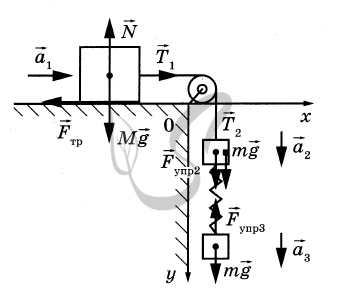
На рисунке показаны силы, действующие на бруски и груз.
Так как блок и нити невесомы, а трение отсутствует, то модули сил натяжения нити, действующих на груз и верхний брусок, одинаковы:
\( \left| {{{\vec T}_1}} \right| = \left| {{{\vec T}_2}} \right| = T \)
Равны по модулю и силы
\( \left| {{F_{упр2}}} \right| = \left| {{F_{упр3}}} \right| \) ,
так как пружина лёгкая.

Решение 1. Запишем второй закон Ньютона в проекциях на оси Ox и Oy выбранной системы координат. С учётом (1)-(3) получим:
\( Ox = M\alpha = T - {F_{тр}} \)
\( Oy = N = Mg,m\alpha = mg - T + {F_{упр}},m\alpha = mg - {F_{упр}} \)
Сложив эти уравнения, найдём ускорение тел: \( a = \frac{{2mg - {F_{тр}}}}{{M + 2m}} \)
2. Сила трения \( {F_{тр}} = \mu N = \mu Mg \)
3. Из последнего уравнения в п. 1 получим \( {F_{упр}} = m(g - a) = \frac{{mMg\left( {1 + \mu } \right)}}{{M + 2m}} \)
По закону Гука \( {F_{упр}} = k\Delta l = k\left( {L - l} \right) \), тогда
\( k = \frac{{mMg\left( {1 + \mu } \right)}}{{\left( {L - l} \right)\left( {M + 2m} \right)}} = \) \( \frac{{0,4 \cdot 0,8 \cdot 10 \cdot \left( {1 + 0,2} \right)}}{{\left( {0,14 - 0,1} \right) \cdot \left( {0,8 + 2 \cdot 0,4} \right)}} = 60 \) Н/м.
Ответ: k = 60 Н/м

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21079.

Обоснование
Задачу будем решать в инерциальной системе отсчёта, связанной с поверхностью стола. Будем применять для грузов и бруска законы Ньютона, справедливые для материальных точек, поскольку тела движутся поступательно. Трением в оси блока и трением о воздух, а также массой блока пренебрежём.
Так как нить нерастяжима и длина пружины постоянна, ускорения обоих брусков и груза равны по модулю:
\( \left| {{{\vec a}_1}} \right| = \left| {{{\vec a}_2}} \right| = \left| {{{\vec a}_3}} \right| = a \)
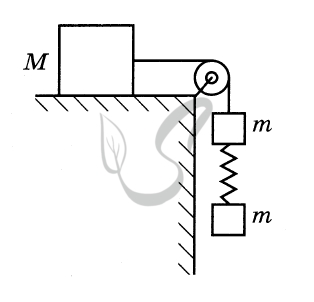
На рисунке показаны силы, действующие на бруски и груз.
Так как блок и нити невесомы, а трение отсутствует, то модули сил натяжения нити, действующих на груз и верхний брусок, одинаковы:
\( \left| {{{\vec T}_1}} \right| = \left| {{{\vec T}_2}} \right| = T \)
Равны по модулю и силы
\( \left| {{F_{упр2}}} \right| = \left| {{F_{упр3}}} \right| \) ,
так как пружина лёгкая.

Решение 1. Запишем второй закон Ньютона в проекциях на оси Ox и Oy выбранной системы координат. С учётом (1)-(3) получим:
\( Ox = M\alpha = T - {F_{тр}} \)
\( Oy = N = Mg,m\alpha = mg - T + {F_{упр}},m\alpha = mg - {F_{упр}} \)
Сложив эти уравнения, найдём ускорение тел: \( a = \frac{{2mg - {F_{тр}}}}{{M + 2m}} \)
2. Сила трения \( {F_{тр}} = \mu N = \mu Mg \)
3. Из последнего уравнения в п. 1 получим \( {F_{тр}} = \mu N = \mu Mg \)
По закону Гука \( {F_{упр}} = k\Delta l = k\left( {L - l} \right) \), тогда
\( L = l + \frac{{mMg\left( {1 + \mu } \right)}}{{k\left( {M + 2m} \right)}} = \) \( 0,1 + \frac{{0,4 \cdot 0,8 \cdot 10 \cdot \left( {1 + 0,2} \right)}}{{80 \cdot \left( {0,8 + 2 \cdot 0,4} \right)}} \) \( = 0,13 \) м.
Ответ: L = 0,13 м

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21078.

Обоснование
1. Задачу будем решать в инерциальной системе отсчёта, связанной со столом. При нахождении ускорений тел будем применять второй закон Ньютона, сформулированный для материальных точек, поскольку тела движутся поступательно.
Трением в оси блока о воздух пренебрежём; блок будем считать невесомым.
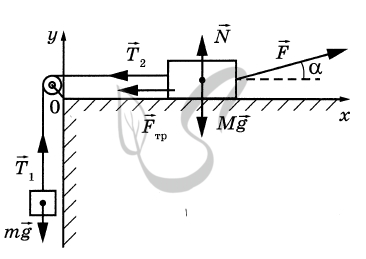
На рисунке показаны силы, действующие на брусок и груз.

2. Так как нить нерастяжима, ускорения бруска и груза равны по модулю:
\( \left| {{{\vec a}_1}} \right| = \left| {{{\vec a}_2}} \right| = a \)
3. Так как блок и нить невесомы и трения в блоке нет, то силы натяжения нити, действующие на груз и брусок, одинаковы по модулю:
\( \left| {{{\vec T}_1}} \right| = \left| {{{\vec T}_2}} \right| = T \)
Решение
1. Запишем второй закон Ньютона в проекциях на оси Ox и Oy выбранной системы координат. Учитывая (1) и (2), получим: \( F\cos \alpha - T - {F_{tr}} = M\alpha , \) , \( N + F\sin \alpha = Mg, \) , \( T - mg = m\alpha \).
Сила трения, действующая на брусок, \( {F_{tr}} = \mu N \).
Решая полученную систему уравнений, найдём ускорение тел:
\( a = \frac{{F\left( {\cos \alpha + \mu \sin \alpha } \right) - mg - \mu Mg}}{{M + m}} \)
2. Так как начальная скорость груза была равна нулю, \( L = \frac{{a{t^2}}}{2} \)
3. Окончательно получим:
\( t = \sqrt {\frac{{2L}}{a}} = \) \( \sqrt {2L\left( {\frac{{M + m}}{{F\left( {\cos \alpha + \mu \sin \alpha } \right) - mg - \mu Mg}}} \right)} = \) \( \sqrt {2 \cdot 0,32 \cdot \left( {\frac{{1 + 0,5}}{{9 \cdot \left( {\frac{{\sqrt 3 }}{2} + 0,3 \cdot 0,5} \right) - 0,5 \cdot 10 - 0,3 \cdot 1 \cdot 10}}} \right)} \) \( \approx 0,92 \) с.
Ответ: t = 0,92 с

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21077.

Обоснование
1. Задачу будем решать в инерциальной системе отсчёта, связанной со столом. При нахождении ускорений тел будем применять второй закон Ньютона, сформулированный для материальных точек, поскольку тела движутся поступательно.
Трением в оси блока о воздух пренебрежём; блок будем считать невесомым.
На рисунке показаны силы, действующие на брусок и груз.

2. Так как нить нерастяжима, ускорения бруска и груза равны по модулю:
\( \left| {{{\vec a}_1}} \right| = \left| {{{\vec a}_2}} \right| = a \)
3. Так как блок и нить невесомы и трения в блоке нет, то силы натяжения нити, действующие на груз и брусок, одинаковы по модулю:
\( \left| {{{\vec T}_1}} \right| = \left| {{{\vec T}_2}} \right| = T \)
Решение
1. Запишем второй закон Ньютона в проекциях на оси Ox и Oy выбранной системы координат. Учитывая (1) и (2), получим: \( F\cos \alpha - T - {F_{тр}} = M\alpha , \) , \( N + F\sin \alpha = Mg, \) , \( T - mg = m\alpha \).
Сила трения, действующая на брусок, \( {F_{тр}} = \mu N \).
Решая полученную систему уравнений, найдём ускорение тел:
\( a = \frac{{F\left( {\cos \alpha + \mu \sin \alpha } \right) - mg - \mu Mg}}{{M + m}} \)
2. Так как начальная скорость груза была равна нулю, \( L = \frac{{{\upsilon ^2}}}{{2a}} \)
3. Окончательно получим:
\( \upsilon = \sqrt {2aL} = \) \( \sqrt {2L\left( {\frac{{F\left( {\cos \alpha + \mu \sin \alpha } \right) - mg - \mu Mg}}{{M + m}}} \right)} = \)\( \sqrt {2 \cdot 0,32 \cdot \left( {\frac{{9 \cdot \left( {\frac{{\sqrt 3 }}{2} + 0,3 \cdot 0,5} \right) - 0,5 \cdot 10 - 0,3 \cdot 1 \cdot 10}}{{1 + 0,5}}} \right)} \) \( \approx 0,7 \) м/с
Ответ: \( \upsilon \approx 0,7 \) м/с

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21076.

Обоснование
1. Систему отсчёта, связанную с Землёй, будем считать инерциальной. Тела можно - считать материальными точками, так как их размеры пренебрежимо малы в условиях задачи.
2. При соударении для системы «пуля - тело» в ИСО выполняется закон сохранения импульса в проекциях на горизонтальную ось, так как внешние силы (сила тяжести и сила реакции опоры) вертикальны.
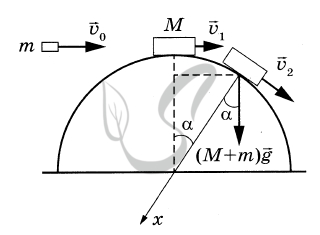
3. При движении составного тела от вершины полусферы выполняется закон сохранения механической энергии, так как полусфера гладкая, и работа силы реакции опоры равна нулю (эта сила перпендикулярна скорости тела).
4. В момент отрыва обращается в нуль сила реакции опоры \( {\vec N} \).
5. Второй закон Ньютона выполняется в ИСО для модели материальной точки.

Решение
1. Закон сохранения импульса связывает скорость пули перед ударом со скоростью составного тела массой m+M сразу после удара: \( m{\upsilon _0} = \left( {m + M} \right){\upsilon _1} \).
Закон сохранения механической энергии связывает скорость составного тела сразу после удара с его скоростью в момент отрыва от полусферы:
\( \frac{{\left( {m + M} \right)\upsilon _1^2}}{2} + \left( {m + M} \right)gR = \) \( \frac{{\left( {m + M} \right)\upsilon _2^2}}{2} + \left( {m + M} \right)gR\cos \alpha \)
где \( {\upsilon _2} \) — скорость составного тела в момент отрыва; \( h = R\cos \alpha \) — высота точки отрыва (см. рисунок).
2. Второй закон Ньютона в проекциях на ось x (направленную в центр полусферы) в момент отрыва тела принимает вид: \( \left( {m + M} \right)g\cos \alpha = \frac{{\left( {m + M} \right)\upsilon _2^2}}{R} \)
3. Объединяя уравнения, получим: \( \frac{{\upsilon _1^2}}{2} + gR = \frac{3}{2}gh \)
Отсюда \( R = \frac{3}{2}h - \frac{1}{{2g}} \cdot {\left( {\frac{{m{\upsilon _0}}}{{M + m}}} \right)^2} = \) \( \frac{3}{2} \cdot 1 - \frac{1}{{2 \cdot 10}} \cdot {\left( {\frac{{0,01 \cdot 200}}{{0,99 + 0,01}}} \right)^2} = 1,3 \) м.
Ответ: R = 1,3 м

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21075.

Обоснование
1. Систему отсчёта, связанную с Землёй, будем считать инерциальной. Тела можно - считать материальными точками, так как их размеры пренебрежимо малы в условиях задачи.
2. При соударении для системы «пуля - тело» в ИСО выполняется закон сохранения импульса в проекциях на горизонтальную ось, так как внешние силы (сила тяжести и сила реакции опоры) вертикальны.
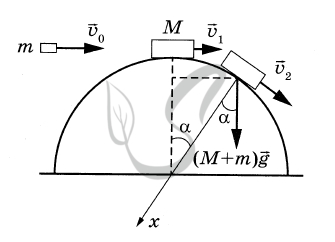
3. При движении составного тела от вершины полусферы выполняется закон сохранения механической энергии, так как полусфера гладкая, и работа силы реакции опоры равна нулю (эта сила перпендикулярна скорости тела).
4. В момент отрыва обращается в нуль сила реакции опоры \( {\vec N} \).
5. Второй закон Ньютона выполняется в ИСО для модели материальной точки.

Решение
1. Закон сохранения импульса связывает скорость пули перед ударом со скоростью составного тела массой m + M сразу после удара: \( m{\upsilon _0} = \left( {m + M} \right){\upsilon _1} \).
Закон сохранения механической энергии связывает скорость составного тела сразу после удара с его скоростью в момент отрыва от полусферы: \( \frac{{\left( {m + M} \right)\upsilon _1^2}}{2} + \left( {m + M} \right)gR \) \( = \frac{{\left( {m + M} \right)\upsilon _2^2}}{2} + \left( {m + M} \right)gR\cos \alpha \)
где \( {\upsilon _2} \) — скорость составного тела в момент отрыва; \( h = R\cos \alpha \) — высота точки отрыва (см. рисунок).
2. Второй закон Ньютона в проекциях на ось x (направленную в центр полусферы), в момент отрыва тела принимает вид:
\( \left( {m + M} \right)g\cos \alpha = \) \( \frac{{\left( {m + M} \right)\upsilon _2^2}}{R} \)
3. Объединяя уравнения, получим: \( \frac{{\upsilon _1^2}}{2} + gR = \frac{3}{2}gh \)
Отсюда \( h = \frac{1}{{3g}} \cdot {\left( {\frac{{m{\upsilon _0}}}{{M + m}}} \right)^2} + \frac{2}{3}R = \) \( \frac{1}{{3 \cdot 10}} \cdot {\left( {\frac{{0,01 \cdot 200}}{{0,99 + 0,01}}} \right)^2} + \frac{2}{3} \cdot 1 = 0,8 \) м.
Ответ: 0,8 м

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21074.

Обоснование
Задачу будем решать в инерциальной системе отсчёта, связанной с поверхностью Земли. Будем считать все тела материальными точками. Трением снаряда и осколков о воздух пренебрежём.
Поскольку время разрыва снаряда мало, импульсом внешних сил (сил тяжести) можно пренебречь, а значит, для решения задачи можно воспользоваться законом сохранения импульса.
Так как при решении задачи мы пренебрегаем силой трения, то можно использовать закон сохранения энергии для снаряда с учётом энергии разрыва.

Решение
1. Запишем законы сохранения импульса и сохранения энергии для снаряда:
\( m{\upsilon _0} = \frac{m}{2}{\upsilon _1} - \frac{m}{2}{\upsilon _2}; \)\( m \cdot \frac{{\upsilon _0^2}}{2} + \Delta E = \frac{{m{\upsilon _1}}}{4} + \frac{{m{\upsilon _2}}}{4}, \)
где \( m \) — масса снаряда до взрыва; \( {\upsilon _0} \) — модуль скорости снаряда до взрыва; \( {\upsilon _1} \) — модуль скорости осколка, летящего вперёд; \( {\upsilon _2} \) — модуль скорости осколка, летящего назад.
2. Выразим \( {\upsilon _0} \) из первого уравнения: \( {\upsilon _0} = \frac{1}{2}\left( {{\upsilon _1} - {\upsilon _2}} \right) \) — и подставим во второе уравнение.
3. Получим: \( m = \frac{{8\Delta E}}{{{{\left( {{\upsilon _1} + {\upsilon _2}} \right)}^2}}} \) \( = \frac{{8 \cdot 600 \cdot {{10}^3}}}{{{{\left( {900 + 100} \right)}^2}}} = 4,8 \) кг
Ответ: \( m \) = 4,8 кг

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21073.

Обоснование
Задачу будем решать в инерциальной системе отсчёта, связанной с поверхностью Земли. Будем считать все тела материальными точками. Трением снаряда и осколков о воздух пренебрежём.
Поскольку время разрыва снаряда мало, импульсом внешних сил (сил тяжести) можно пренебречь, а значит, для решения задачи можно воспользоваться законом сохранения импульса.
Так как при решении задачи мы пренебрегаем силой трения, то можно использовать закон сохранения энергии для снаряда с учётом энергии разрыва.
Решение
1. Запишем законы сохранения импульса и сохранения энергии для снаряда:
\( 2m \cdot {\upsilon _0} = m{\upsilon _1} - m{\upsilon _2}, \)\( 2m \cdot \frac{{\upsilon _0^2}}{2} + \Delta E = \frac{{m\upsilon _1^2}}{2} + \frac{{m\upsilon _2^2}}{2} \)
где \( 2m \) - масса снаряда до взрыва; \( {\upsilon _0} \) - модуль скорости снаряда до взрыва; \( {\upsilon _1} \)- модуль скорости осколка, летящего вперёд; \( {\upsilon _2} \) — модуль скорости осколка, летящего назад.

2. Выразим \( {\upsilon _0} \) из первого уравнения: \( {\upsilon _0} = \frac{1}{2}\left( {{\upsilon _1} - {\upsilon _2}} \right) \) - и подставим во второе уравнение.

3. Получим: \( \Delta E = \frac{m}{4}{\left( {{\upsilon _1} + {\upsilon _2}} \right)^2} = \)\( \frac{1}{4}{\left( {900 + 1000} \right)^2} = 250 \)
Ответ: \( \Delta E = 250 \)

P.S. Нашли ошибку в задании? Пожалуйста, сообщите о вашей находке ;)
При обращении указывайте id этого вопроса - 21072.